Entrainement : Bases de l’optique
Contents
Entrainement : Bases de l’optique#
Ces exercices seront traités en classe.
Fibre optique à saut d’indice#
Objectifs: Établir les expressions du cône d’acceptance et de la dispersion intermodale d’une fibre à saut d’indice.
Une fibre optique à saut d’indice est constituée d’un coeur en silice d’indice \(n_1\) entouré d’une gaine d’indice \(n_2\). Le tout est à symétrie cylindrique. Elle permet de transporter des informations par modulation d’amplitude d’un faisceau lumineux confiné à l’intérieur de la fibre par réflexion totale.
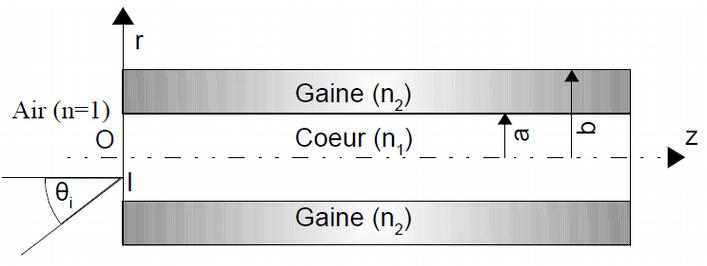
Fig. 2 Fibre optique#
La perte en transmission (ou atténuation) \(X\) s’exprime par \(X_{dB}=10\log(\frac{P_2}{P_1})\) avec \(P_1\) la puissance lumineuse à l’entrée de la fibre et \(P_2\) la puissance lumineuse au bout d’un kilomètre dans la fibre. On l’exprime en \(\rm{dB.km^{-1}}\)
Exercice
Quelle condition doit-on imposer à \(n_2\) et \(n_1\) pour pouvoir confiner la lumière dans la fibre (c’est-à-dire pour qu’il y ait réflexion totale) ?
Sachant qu’en 1970, l’atténuation était de \(-10\rm{dB.km^{-1}}\) et qu’actuellement elle est de \(-0.005\rm{dB.km^{-1}}\), déterminer dans les deux cas les pertes en puissance en % au bout d’un km.
Un rayon lumineux arrive en I avec un angle \(\theta_i\). Montrer que si \(\theta_i\) est inférieur à un angle \(\theta_a\), un rayon peut être guidé à travers le coeur. Pour une fibre cylindrique, justifier le terme de cône d’acceptance.
On appelle ouverture numérique (O.N.) la grandeur \(\sin(\theta_a)\). Donner l’expression de O.N. en fonction de \(n_1\) et de \(\Delta=\frac{n_1^2-n_2^2}{2n_1^2}\). A.N.: \(\Delta=10^{-2},n_1=1,5\).
Une impulsion lumineuse (une information) arrive à t = 0 au point O sous la forme d’un faisceau conique de demi-angle au sommet (O) \(\theta_i\) (\(\theta_i<\theta_a\)).
Pour une fibre de longueur l, calculer l’élargissement temporel (ou dispersion intermodale) \(\Delta t\) à la sortie de la fibre, c’est-à-dire le temps écoulé entre la sortie du premier rayon et celle du dernier. On l’exprimera en fonction de \(l, n_1, c\) et \(\theta_i\).
En déduire quelle quantité d’information cette fibre peut transmettre en une seconde. A.N.: \(l=10km,\theta_i=8^{\circ},n_1=1,5\)
Point utile pour cet exercice
\(\Longrightarrow\) Lois de Snell-Descartes.
\(\Longrightarrow\) Réflexion totale.
Eléments de réponse (sans justification)
\(n_2 < n_1\)
90% puis 0.1%
\(\theta_a = \arcsin{\sqrt{n_1^2 - n_2^2}}\)
\(sin \theta_a = n_1 \sqrt{2 \Delta} = 0.2\)
\(\Delta t = \frac{n_1 l}{c} \left( \frac{1}{\sqrt{1 - {\left(\frac{\sin \theta_i}{n_1}\right)}}^2} - 1 \right)\)
\(\Delta t = 50 \rm{\mu s} \)
TD: Arc-en-ciel#
On désire étudier le phénomène de l’arc-en-ciel au moyen d’un modèle simple. On suppose ici que les gouttes d’eau sont assimilables à des sphères de rayon R, de centre O et d’indice de réfraction homogène n = 1,3 baignant dans l’air.
La sphère est éclairée par un faisceau de lumière parallèle, dont un rayon atteint la sphère en A. Après réfraction, le rayon retouche le dioptre eau-air en B. Le rayon alors réfléchi recoupe la sphère en C où un rayon refracté ressort avec une angle \(\widehat{a}\) par rapport à l’axe Ox. On pose \(\widehat{i}\) l’angle incident au point A et \(\widehat{r}\) l’angle réfracté au même point A (c’est-à-dire l’angle \(\widehat{OAB}\)). On supposera que \(\widehat{a} \in [0;\pi/2 ]\).
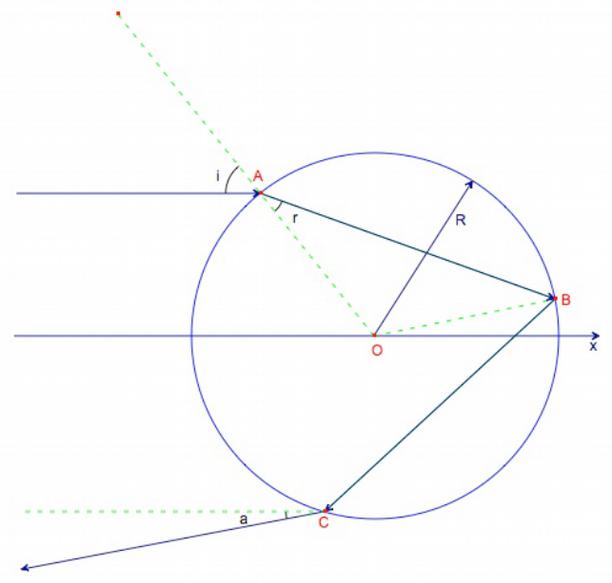
Fig. 3 Arc-en-ciel#
Exercice
Pourquoi suppose-t-on que le faisceau incident est un faisceau de rayons parallèles ? Quelle est sa direction ?
Quelles sont alors les valeurs possibles de l’angle \(\widehat{i}\) ?
Peut-il y avoir réflexion totale en B?
Montrer que \(\widehat{a}=4\widehat{r}-2\widehat{i}\).
En déduire \(\widehat{a}\) en fonction de \(\widehat{i}\) seulement.
Calculer \(\frac{d\widehat{a}}{d\widehat{i}}\)
Montrer qu’il existe un angle \(i_{\max}\) pour lequel \(\widehat{a}\) est maximal. Calculer \(i_{\max}\) et \(a_{\max}\).
Montrer que si un observateur regarde haut dans le ciel avec un angle \(\widehat{a}\) qu’on précisera, il recevra un maximum de lumière (il y aura accumulation des rayons lumineux).
Eléments de réponse (sans justification)
…
\([-\pi/2;\pi/2]\)
Non
…
\(a = 4 \arcsin\frac{\sin i}{n} - 2 i\)
\(\frac{\rm{d}a}{\rm{di}} = 4 \frac{\frac{\cos i}{n}}{\sqrt{1 - \frac{\sin^2 i}{n^2}}} - 2\)
\(i_{\max} = \arccos\sqrt{ \frac{n^2-1}{3}} = 1.07 \rm{rad}\) et \(a_{\max} = 0.82 \rm{rad}\)
Cet observateur ne verra alors les gouttes “briller” que sur un cône d’axe de révolution (observateur-direction des rayons provenant du soleil) et de demi-angle au sommet (qui est l’observateur) \(a_{\max}\). Généralement l’horizon empêche d’observer complètement le cône.
Exercice
Dans des conditions telles que le soleil soit à l’ouest, incliné de \(10^{\circ}\) au-dessus de l’horizon. De quel côté faut-il regarder pour observer un arc-en-ciel? Préciser la hauteur angulaire maximale \(\alpha\) au-dessus de l’horizon et les circonstances météorologiques nécessaires à l’observation.
On explique le phénomène de l’arc-en-ciel par les propriétés dispersives de l’eau, c’est-à-dire que l’indice de réfraction de l’eau varie en fonction de la longueur d’onde de la lumière.
Déterminer les valeurs maximum de a pour le rouge (n=1,331) et pour le violet (n=1,337) et en déduire quelle couleur fera l’extérieur de l’arc-en-ciel (c’est-à-dire la partie la plus haute). Que vaut l’ouverture angulaire \(\Delta\alpha\) de l’arc-en-ciel?
Point utile pour cet exercice
\(\Longrightarrow\) Lois de Snell-Descartes.
\(\Longrightarrow\) Réflexion totale.
\(\Longrightarrow\) Trigonométrie
Eléments de réponse (sans justification)
Soleil dans le dos, sous un angle \(a_{\max} - \alpha\)
La déviation par le prisme#
Il s’agit d’une activité d’approfondissement permettant d’essayer de s’entraîner sur un exercice plus difficile. Certains points pourront être utiles plus tard en Travaux Pratiques.
Principe général: On considère un prisme triangulaire d’angle au sommet A dont la base est posée horizontalement sur un socle. On envoie un faisceau lumineux constitué de rayon parallèle sur une des face et on observe les rayons sortant par l’autre face (les deux faces constituant l’angle A). Ce seront les deux faces utiles du prisme. Le faisceau étant parallèle l’angle que font les rayons avec la première face du prisme est toujours la même, on note cet angle i. Il vient par les lois de Descartes que les angles formées par les différents rayons réfractés seront les mêmes quelques soit le rayon considéré. On va donc considérer un seul rayon pour l’étude.
But: On désire étudier la déviation du rayon lumineux D en fonction de l’angle d’incidence i. L’air extérieur est considéré comme un milieu d’indice 1.
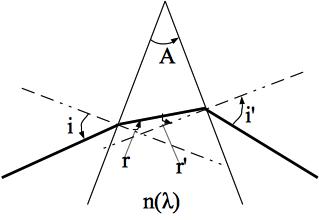
Fig. 4 Déviation par le prisme#
Exercice
Etablir une relation entre i,r et n puis entre i’, r’ et n.
Montrer que \(A=r+r'\) et \(D=i+i'-A\).
Existence d’un rayon dévié.
*Quelles sont les valeurs de i telles qu’on observe effectivement un rayon sortant du prisme? On ne tiendra pas compte des limitations géométriques du prisme. Déterminer cette gamme pour \(n=1,5\) et \(A=60^{\circ}\). On notera \(i_0\), l’angle limite qui apparaî dans le raisonnement.
Que se passe-t-il si l’angle du prisme est trop grand (\(90^{\circ}\) par exemple)?
Faire un tracé des rayons et déterminer l’angle de déviation D pour les cas \(i=i_0\) et \(i=\pi/2\). Commenter.
Déduire de la question précédente que la fonction \(D(i)\) passe par au moins un extremum. L’expérience montre qu’il y en a qu’un seul et que c’est un minimum de déviation. On notera \(D_m\) le minimum de déviation.
*Retrouver le résultat de l’expérience par une étude mathématique de la fonction \(D(i)\).
Quelle est la relation entre \(D_m\), A et n?
En général, le prisme choisi est très dispersif c’est-à-dire que l’indice de réfraction n dépend fortement (tout est relatif) de la longueur d’onde du faisceau incident \(\lambda\). Expliquer pourquoi un tel dispositif permet la réaliser d’un spectroscope, c’est-à-dire un appareil permettant de déterminer le spectre d’un signal lumineux.
(Recherche) Expliquez comment Newton a utiliser cette méthode pour montrer que la lumière blanche était composé d’un grand nombre de radiations “élémentaires”. Commenter ce terme (et précisez le terme utilisé aujourd’hui).
Point utile pour cet exercice
\(\Longrightarrow\) Lois de Snell-Descartes.
\(\Longrightarrow\) Réflexion totale.
\(\Longrightarrow\) Trigonométrie
Correction
Voici la correction complète de cet exercice, elle servira pour un TP ultérieur.
Fig. 5 Déviation par le prisme#
1. Les loi de Snell-Descartes pour la réfraction en I et I’ s’écrivent:
2. Dans le quadrilatère AIHI’, la somme des angles s’écrit \(\widehat{IHI'} + \frac{\pi}{2} + A + \frac{\pi}{2} = 2 \pi\) et dans le triangle IHI’ \(\widehat{IHI'} + r + r' = \pi\). Il vient:
De plus dans le quadrilatère GIHI’ : \(\widehat{IHI'} + i + (\pi - D) + i' = 2 \pi\). Il vient:
3. Lorsque i augmente, r augmente et r’ diminue donc i’ diminue. Il vient que le cas de réflexion totale risque d’arriver pour des angles \(i\) faibles. La limite de réflexion totale est pour \(r' = \arcsin \frac{1}{n}\) soit \(r = A - \arcsin \frac{1}{n}\) soit:
Les gammes de valeurs permettant d’avoir un rayon sortant sont donc \(i_0 \leq i \leq \frac{\pi}{2}\). A.N. : \(i_0 = 28 ^{\circ}\)
Si l’angle \(A\) est trop grand, \(i_0\) n’est pas défini: tous les angles \(i\) donnent une réflexion totale, on parle de “prisme à réflexion totale” (utilisé dans les jumelles par exemples).
Si \(i=i_0\), alors \(i'=\frac{\pi}{2}\) soit \(D = i_0 + \frac{\pi}{2} - A\). Si \(i=\frac{\pi}{2}\), alors \(i'=i_0\) soit \(D = i_0 + \frac{\pi}{2} - A\).
4. \(D(i)\) étant une fonction continue non constante et \(D(i_0) = D(\pi/2)\), il vient qu’il y a forcément un extremum entre les deux.
5. On calcul \(\frac{\rm{dD}}{\rm{di}}\):
Or, des différentes relations précédentes, il vient:
donc:
Au cas extrême \((i=i_0, i'=\pi/2)\), \(D = -\infty\). Au cas extrême \((i'=i_0, i=\pi/2)\), \(D = 1\).
Donc, la dérivée s’annule forcément, il y aura au moins un extremum et au moins un minimum (passage d’une valeur négative à une valeur positive).
6. Sous l’hypothèse d’unicité, il vient que \(i=i'\) au minimum de déviation \(D_m\) (sinon si \(i=i_1 \neq i' = i_2\) pour \(D = D_m\), alors \(D=D_m\) pour \(i=i_2; i' = i_1\) par retour inverse et relation trouvée précédemment : il n’y aurait pas unicité). Il vient (on pose \(i = i_m\) et \(r = r_m\) au minimum de déviation):
soit avec Snell-Descartes:
7. L’indice de réfraction dépendant de la longueur d’onde, ces dernières seront séparées par le prisme. L’indice de réfraction étant propre au prisme comme l’angle A, il vient qu’en utlisant une lampe dont les longueurs d’onde sont connues, on peut associer à différentes longueurs d’onde un angle de déviation minimal \(D_{m,i}(\lambda_i)\) puis par interpolation la fonction \(D_m(\lambda)\). On peut ensuite utiliser cette courbe d’étalonnage pour, en mesurant un angle de déviation \(D_m\), remonter à une longueur d’onde inconnue.
8.”élémentaires” = “monochromatique”. Il a placé un deuxième prisme après le premier en ayant isolé une couleur: celle-ci ne se séparait pas à nouveau en plusieurs couleurs contrairement à la lumière différenciant ainsi une lumière polychromatique d’une lumière monochromatique.