Lois de Snell-Descartes - Méthodes¶
Méthode: Tracé qualitatif du rayon réfracté.¶
Le tracé du rayon réfléchi s’obtient par simple symétrie quel que soient les valeurs des indices. Nous allons plutôt ici voir comment on peut prévoir semi-qualitativement le tracé du rayon réfracté et nous obtiendrons plus informations très importantes. Nous travaillerons dans le plan d’incidence.
Les conclusions obtenues ici sont à connaître autant qu’à savoir retrouver.
Il est vivement conseillé de réfléchir aux exercices avant de regarder les réponses (en ligne).
Exercice
On considère le cas où \(n_1 < n_2 \).
Le rayon réfracté s’éloigne-t-il ou se rapproche-t-il de la normale?
Justifier que l’angle réfracté ne peut prendre qu’une gamme de valeur limitée dans le plan d’incidence.
Correction
Tracé qualitatif du rayon réfracté
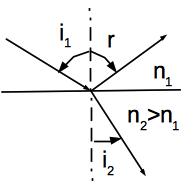
Remarquons que \(\frac{\sin i_1}{\sin i_2} = \frac{n_2}{n_1} > 1\). Or sur \([-\pi;\pi/2]\), la fonction sinus est croissante donc \(i_1> i_2\).
Il vient qu’au passage d’un milieu moins réfringent à un milieu plus réfringent, le rayon réfracté se rapproche de la normale.
Gamme d’angle
L’étude précédente montre que quand l’angle d’incidence atteint \(\pi/2\) (on parle d’incidence rasante), l’angle réfracté est encore inférieur l’angle droit. Il apparaît que les gammes d’angles en sortie sont limitées. On atteint pas toutes les valeurs entre \(-\pi/2\) et \(\pi/2\).
Plus précisément, les gammes valeurs atteintes sont \(i_2 \in [-\arcsin\left ( \frac{n_1}{n_2}\right); \arcsin\left ( \frac{n_1}{n_2}\right)]\)
Important
On retiendra que lors du passage d’un milieu moins réfringent à un milieu plus réfringent:
le rayon réfracté se rapproche de la normale par rapport au rayon incident
le rayon réfracté va avoir une gamme limitée de valeur. La valeur limite \(i_2 =\arcsin\left ( \frac{n_1}{n_2}\right)\) est appelée angle de réfraction limite.
Exercice
On considère le cas où \(n_2 < n_1 \).
Le rayon réfracté s’éloigne-t-il ou se rapproche-t-il de la normale?
Justifier que l’angle réfracté va atteinte une réfraction rasante (égale à \(\pm \pi/2\) pour un angle d’incidence strictement inférieure à \(\pm \pi/2\) (en valeur absolue). On notera \(i_0\) la valeur limite de l’angle d’incidence.
Que se passe-t-il si l’angle d’incidence est supérieure à \(i_0\) ?
Correction
Tracé qualitatif du rayon réfracté
Remarquons que \(\frac{\sin i_1}{\sin i_2} = \frac{n_2}{n_1} < 1\). Or sur \([-\pi;\pi/2]\), la fonction sinus est croissante donc \(i_1 < i_2\).
Il vient qu’au passage d’un milieu moins réfringent à un milieu plus réfringent, le rayon réfracté s’éloigne de la normale
Gamme d’angle
L’étude précédente montre que quand l’angle de réfraction atteint \(\pm \pi/2\), l’angle d’incidence est encore inférieur l’angle droit. L’angle limite d’incidence est \(i_0 = \pm \arcsin\left ( \frac{n_2}{n_1}\right)\).
Réflexion totale
Si l’angle d’incidence est supérieure à \(i_0\), on observe expérimentalement qu’il n’y a pas de rayon réfracté. On parle de réflexion totale: toute la lumière est réfléchie.
Important
On retiendra que lors du passage d’un milieu plus réfringent à un milieu moins réfringent:
le rayon réfracté s’éloigne de la normale par rapport au rayon incident
si l’angle d’incidence devient trop grand, il y a phénomène de réflexion totale, c’est-à-dire que toute la lumière est réfléchie.
L’angle d’incidence limite permettant la réfraction se calcule en cherchant un angle réfracté de \(\pm \pi/2\). On obtient:
Exemple : Utilisation des lois de Snell-Descartes¶
La correction est en ligne.
Exercice
On considère une pièce de monnaie de rayon \(R_0\) dont on négligera l’épaisseur posée au fond d’une casserole de hauteur \(H_0\) remplie à ras bord d’eau.
L’oeil d’un observateur se trouve à la verticale de centre de la pièce à une hauteur \(H_1\).
On appelle O le centre de la pièce. Déterminer l’équation que vérifie l’ouverture angulaire \(\theta_0\) du faisceau issu du point O et qui entre dans l’oeil en fonction du rayon de la pupille \(R_1\).
**Faire l’application numérique pour \(H_0 = H_1\) en choisissant des valeurs numériques plausibles. On sera amener à simplifier l’équation précédente AVANT de la résoudre en justifiant les simplification réalisée par des ordres de grandeurs.
Correction
Mise en équation
Notons le point I, le point d’incidence sur le dioptre air-eau pour le rayon extrême du faisceau issu de O et entrant dans la pupille. On note \(i_1\) et \(i_2\) les angles respectivement d’incidence et de réfraction. On a les relations :
\[\begin{align*} n_{eau} \sin i_1 &= n_{air} \sin i_2\\ \frac{IL}{\tan i_2} &= H_1\\ IL + IJ &= R_1\\ \tan i_1 &= \frac{IJ}{H_0} \end{align*}\]On a 4 inconnues (IL, IJ, \(i_1\) et \(i_2\)) et quatre inconnues, on peut donc résoudre le système.
Il est important de voir que la résolution complète ne nous intéresse pas. On veut \(i_1\) qui représente l’ouverture angulaire. On va donc chercher à garder \(i_1\) et éliminer les autres inconnues.
Les grandeurs \(H_0, H_1, R_1\) et les indices sont des grandeurs connues qu’on va garder.
Equation pour l’angle: Les deux dernières équations permettent d’écrire: \(IJ = H_0 \tan i_1\) et \( IL = R_1 - H_0 \tan i_1\) d’où le système:
\[\begin{align*} n_{eau} \sin i_1 &= n_{air} \sin i_2\\ \frac{R_1}{\tan i_2} - H_0 \frac{\tan i_1}{\tan i_2}&= H_1 \end{align*}\]soit en éliminant \(i_2\) (on a directement utilisant \(n_{air} = 1\) - on peut se le permettre car l’indice de réfraction est sans dimension: le changer par sa valeur numérique n’impacte pas l’analyse dimensionnelle):
(3)¶\[\begin{equation} \left ( R_1 - H_0 \tan i_1 \right )\sqrt{1 - n_{eau}^2 \sin^2 i_1} = H_1 n_{eau} \sin i_1 \end{equation}\]On rappelle que \(\theta_0 = i_1\)
Résolution aux petits angles
Nous allons faire une approximation pour résoudre cette équation (sans quoi la résolution devient TRÈS délicate). En effet, la taille de la pupille est de l’ordre du mm (on prendra \(R_1 = 1\rm{mm}\)) et la hauteur de la casserole est de l’ordre de la dizaine de cm. (on prendre \(R_0 = 5\rm{cm}\)). Il vient que les angles à la normale seront nécessairement petit.
On peut avoir un ordre de grandeur en considérant que \(\theta_0 \sim \arctan\frac{R_0}{2H_0} \sim 10^{-2} \rm{rad}\). En pratique, la propagation n’est pas rectiligne mais les angles \(i_1\) et \(i_2\) sont nécessairement du même ordre de grandeur que \(\theta_0\).
Or si \(\theta_0 << 1\), on peut faire les approximations dites des petits angles :
\[\begin{align*} \sin i &\approx i\\ \tan i &\approx i\\ \cos i &\approx 1\\ \end{align*}\]On ne conservera pas aussi les puissances au carré des petits angles (on parle d’approximation à l’ordre 1), des précisions seront données sur cette approximation dans des cours ultérieurs. On essaiera déjà d’appréhender la méthode d’utilisation de cette approximation.
Ici l’équation devient :
(4)¶\[\begin{equation} \left ( R_1 - H_0 i_1 \right ) = H_1 n_{eau} i_1 \Longrightarrow \theta_0 = i_1 \approx \frac{R_1}{H_0 + H_1} = 10^{-2} \rm{rad} \end{equation}\]