Contents

Relations des lentilles minces

Lentilles minces: Relations de conjugaison

Lentilles minces: Relation de conjugaison (Enoncé)

Important

Soit une lentille mince de centre optique O, de foyer objet F, de foyer image F’ et de distance focale image f’. Soit un point objet A sur l’axe optique conjugué avec un point image A’. On a les relations suivantes:

  • Relation de Descartes:

(7)\[\begin{equation} \frac{1}{\overline{OA'}} - \frac{1}{\overline{OA}} = \frac{1}{f'} \end{equation}\]

  • Relation de Newton:

(8)\[\begin{equation} \overline{FA} \times \overline{F'A'} = - f'^2 \end{equation}\]

Lentilles minces: Relations de conjugaison (Démonstration)

Important

Démonstration La démonstration passe par plusieurs étapes:

  1. Réaliser un schéma clair avec des rayons utiles mettant en avant des triangles semblables

  2. établir des relations entre les rapports des grandeurs en utilisant les triangles semblables

  3. Isoler les rapports de grandissement \(\frac{\overline{A'B'}}{\overline{AB}}\).

  4. Déduire des équations obtenues les expressions voulues.

1. Nous allons le démontrer pour une lentille convergente. Il faut s’entraîner à le démontrer pour une lentille divergente. Le schéma de construction est donné ci-dessous. On utilise trois rayons entrant:

  • celui passant par le centre optique qui ressort non dévié.

  • celui passant par le foyer principal objet qui ressort parallèle à l’axe optique

  • celui entrant parallèlement à l’axe optique et ressortant en passant par le foyer principal image.

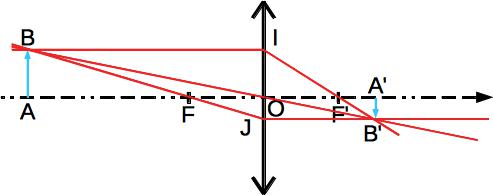
../_images/optique_lentille_conjugaison.jpg

__2.__On remarque que:

  • les triangles OAB et OA’B’

  • les triangles F’OI et F’A’B’

  • les triangles FAB et FOJ

sont tous semblables deux à deux. On peut donc écrire l’ égalité des rapports:

\[\begin{align*} \frac{\overline{AB}}{\overline{OA}} &= \frac{\overline{A'B'}}{\overline{OA'}}\\ \frac{\overline{AB}}{\overline{FA}} &= \frac{\overline{OJ}}{\overline{FO}}\\ \frac{\overline{A'B'}}{\overline{F'A'}} &= \frac{\overline{OI}}{\overline{F'O}} \end{align*}\]

__3.__soit les grandissements (en remarquant que \(\overline{OI} = \overline{AB}\) et \(\overline{OJ} = \overline{A'B'}\)):

\[\begin{align*} \frac{\overline{A'B'}}{\overline{AB}} &= \frac{\overline{OA'}}{\overline{OA}}\\ \frac{\overline{A'B'}}{\overline{AB}} &= \frac{\overline{FO}}{\overline{FA}}\\ \frac{\overline{A'B'}}{\overline{AB}} &= \frac{\overline{F'A'}}{\overline{F'O}} \end{align*}\]

__4.__En égalisant les deux dernières relations, il vient directement (avec \(\overline{FO} = - \overline{F'O} = f')\):

(9)\[\begin{equation} \overline{FA} \times \overline{F'A'} = - f'^2 \end{equation}\]

On peut aussi égaler les deux premières et utiliser la relation \(\overline{FA} = \overline{FO} + \overline{OA}\):

\[\begin{align*} &\overline{OA'} \left(\overline{FO} + \overline{OA}\right) = \overline{FO} \times \overline{OA} \\ &\Longrightarrow \overline{FO} \cdot \overline{OA} - \overline{OA'} \cdot \overline{FO} = \overline{OA'} \cdot \overline{OA} \end{align*}\]

En divisant par le produit \(\overline{OA}\cdot \overline{OA'}\cdot \overline{FO}\), il vient bien la relation:

(10)\[\begin{equation} \frac{1}{\overline{OA'}} - \frac{1}{\overline{OA}} = \frac{1}{f'} \end{equation}\]

Lentilles minces: Relations de grandissement

Important

Soit une lentille mince de centre optique O, de foyer objet F, de foyer image F’ et de distance focale image f’. Soit un objet AB dans un plan frontal conjugué avec une image A’B’. On a les relations dites de grandissement suivantes:

\[\begin{align*} \frac{\overline{A'B'}}{\overline{AB}} &= \frac{\overline{OA'}}{\overline{OA}}\\ \frac{\overline{A'B'}}{\overline{AB}} &= \frac{\overline{FO}}{\overline{FA}}\\ \frac{\overline{A'B'}}{\overline{AB}} &= \frac{\overline{F'A'}}{\overline{F'O}} \end{align*}\]

Ces relations ont été démontrées lors de l’établissement des relations de conjugaison.

previous

Lentilles minces - Relations

next

Exemples d’études