L’oeil et ses défauts¶
Objectifs
Modéliser l’oeil comme l’association d’une lentille de vergence variable et d’un capteur fixe.
Connaître les ordres de grandeur de la limite de résolution angulaire et de la plage d’accommodation.
L’oeil: Modélisation¶
L’oeil: Eleménts et modélisation¶
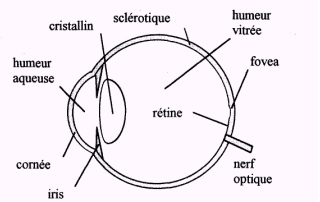
D’un point de vue optique, on distingue plusieurs éléments de l’oeil (cette liste n’est pas exhaustive mais elle suffit à notre étude).
La rétine: constituée des cellules rétiniennes et reliée au nerf optique (qui apporte les information au cerveau). C’est l’endroit où l’image doit se former nettement.
Le cristallin: corps vitreux sur le devant de l’oeil. C’est “le système centré” qui sert à dévié les rayons pour former une image de l’objet visé sur la rétine.
La pupille: devant le cristallin, elle joue le rôle de diaphragme, notamment pour éviter de saturer les cellules rétiniennes en lumière. \end{itemize}
Important
Fondamental : Modélisation optique de l’oeil
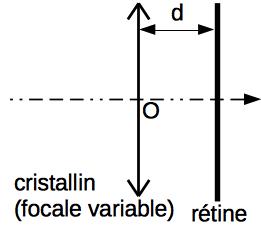
Du point de vue de l’optique géométrique, on peut modéliser l’oeil comme une lentille (le cristallin) diaphragmée (par la pupille) - celle-ci ne sera pas toujours représentée. La lentille est située en amont d’un écran (la rétine) situé à une distance d (en général d=2.5cm pour un oeil emmétrope - oeil normal).
L’oeil: Accomodation¶
Important
Fondamental : Principe d’accomodation
Lorsque l’oeil vise un objet, il doit adapter sa distance focale pour former nettement l’image de l’objet visé sur la rétine. On parle d’accomodation.
L’accomodation de l’oeil se fait grâce à des muscles qui vont déformer le cristallin et changer sa distance focale.
Important
Définition : Punctum Remotum
L’oeil ne peut voir plus loin qu’un point appelé Punctum Remotum. Lorsqu’il vise ce point, les muscles de l’oeil sont relâché et ne se fatiguent pas. On dit que l’oeil est au repos.
Remarque : Accomodation et fatigue oculaire
On pourra compléter la remarque précédente en remarquant que plus l’objet se rapproche de l’oeil, plus les muscles doivent bomber le cristallin ce qui occasionne une fatigue oculaire d’autant plus grande.
Important
Définition : Punctum Proximum L’oeil ne peut voir plus près qu’un point appelé Punctum Proximum (car c’est la configuration où le cristallin est bombé au maximum).
Exemple : Oeil emmétrope
L’oeil emmétrope ou oeil normal est considéré comme la norme lorsqu’il s’agit d’étudier un oeil (on parle aussi d’oeil sans défaut) ou de construire et d’évaluer un instrument d’optique (cf. suite). Ses caractéristiques sont les suivantes:
Le punctum Remotum est à l’infini.
Le punctum Proximum est à une distance d = 25 cm
Les défauts de l’oeil¶
Voici une présentation succincte des différents défauts de l’oeil. Il ne s’agit pas de connaître par coeur les causes possibles mais de savoir que des défauts peuvent exister.
Oeil myope
Un oeil myope est un oeil qui ne peut pas voir de loin. Le Punctum Remotum est ramené à une distance proche (quelque fois quelques dizaines de centimètres).
En général, la myopie est due à une cavité oculaire plus grande que la normale (myopie axiale) mais il arrive qu’elle soit liée à une augmentation de l’indice de réfraction du cristallin (myopie d’indice).
Oeil hypermétrope
Un oeil hypermétrope au repos à tendance à faire converger les rayons derrière la rétine. Cela est souvent dû à une cavité oculaire trop petite.
La conséquence est que l’oeil n’est jamais au repos puisqu’il doit sans cesse accommoder pour voir l’objet visé, même à l’infini. Cela entraîne souvent une fatigue oculaire plus fréquente.
Presbytie
La presbytie, en général liée à l’âge, est la difficulté de voir de près. En général, cela est lié à une fatigue musculaire empêchant de bomber le cristallin suffisamment.
Astigmatie
L’astigmatie est un défaut dans la symétrie axiale de l’oeil qui conduit à donner d’un point objet une image sous forme de tâche. Les images peuvent alors paraître déformée ou floue et entraîne une fatigue oculaire.
Les caractéristiques de l’oeil¶
Caractéristiques de l’oeil: champ angulaire¶
Important
Définition : Champ angulaire, dropdown On définit le champ angulaire de l’oeil (ou d’un instrument d’optique) comme l’angle d’observation maximale.
Exemple : Champ angulaire de l’oeil
Le champ angulaire d’un oeil est d’environ \(160^\circ\) à \(180^\circ\). Il est en pratique limité d’un côté par la présence du nez.
Le champ de vision binoculaire est d’environ \(120^\circ\) mais le champ dans lequel on discrimine les couleurs, celui où l’on peut reconnaître des symboles ou encore celui où l’on peut lire des inscriptions est plus faible.
La donnée du champ angulaire est surtout culturel. On pourra néanmoins dans des cas précis d’instruments scientifiques (comme l’appareil photographique) être amené à déterminer géométriquement et par le calcul un champ angulaire (de l’appareil photo par exemple).
Caractéristique de l’oeil: Résolution angulaire¶
Résolution angulaire
La résolution angulaire est l’écart angulaire minimale entre deux objets peuvent être distinguer par l’oeil. On parle aussi de pouvoir de résolution.
Exemple : Résolution angulaire de l’oeil seul.
La résolution angulaire de l’oeil seul est de l’ordre de \(3 \times 10^{-4} \rm{rad}\).
La résolution angulaire est due à l’existence de cellule rétinienne dont la taille est finie. Si deux objets proches forment une image sur la même cellule rétinienne, ils ne seront pas distingués.
En pratique la diffraction par la pupille limite aussi la résolution angulaire.
Caractéristiques de l’oeil: Profondeur de champ¶
Profondeur de champ
La profondeur de champ est l’intervalle de position donnant une image considérée comme nette par l’instrument (ici l’oeil) pour une configuration (un réglage) de l’instrument (ici pour une valeur de focale du cristallin).
Remarque : Pourquoi y a-t-il une profondeur de champ?
On peut se poser la question car en effet, le stigmatisme et l’aplanétisme prévoit la conjugaison d’un objet à une image et la conjugaison du plan de la rétine avec un seul plan (celui de l’objet visé).
La raison vient du fait que l’oeil n’a pas besoin de former un point sur la rétine pour voir l’objet net ! En effet, l’oeil est constitué de cellules rétiniennes qui ont une taille finie. Si la tâche (au lieu du point) formé est plus faible que la cellules rétiniennes, l’oeil verra l’objet net même s’il n’y a pas conjugaison au sens de l’optique géométrique.
Cette “imperfection” de l’oeil (elle limite la résolution) est très utile puisqu’elle permet de voir des objets nets alors qu’ils ne sont pas dans le même plan: c’est la profondeur de champ.
Profondeur de champ et appareil photographique
Il y a le même phénomène dans un appareil photographique (taille des tâches formées sur la pellicule pour l’argentique ou taille des récepteurs CCD pour le numérique).
Dans ce cas là aussi, cela permet d’avoir une profondeur de champ. Ceux qui ont fait un peu de photographie pourront associer la profondeur de champ à l’ouverture (diaphragme) de l’appareil photographique. Il en est de même pour l’oeil (rôle de la pupille).
Oeil au repos et instruments d’optique¶
Important
Fondamental : Principe de construction et d’étude d’un instrument d’optique
Lorsqu’un fabricant va construire un instrument d’optique, il va chercher à assurer un confort visuel. Pour celà, il va faire en sorte que l’image finale soit au Punctum Remotum pour l’utilisateur.
Remarque
Adaptation aux différents yeux et données commerciales.
Lorsqu’un constructeur fournit des informations sur son appareil, il suppose qu’il est utilisé en condition optimale par un oeil emmétrope, c’est-à-dire que l’image finale donnée par l’instrument d’optique (lunette astronomique, telescope, loupe… ) est à l’infini. On parle de données “commerciales”. Nous étudierons souvent les instruments d’optique dans ces conditions.
Comme on l’a vu, le Punctum Remotum peut être à des endroit différents suivant l’utilisateur. C’est pourquoi la majorité des appareils offrent un réglage permettant d’adapter l’appareil à l’utilisation par une personne myope par exemple.
Application: accomodation de l’oeil¶
Cet exercice d’application directe est à faire à la suite du cours pour vérifier votre compréhension des méthodes. Vous pourrez confronter votre travail avec celui de vos camarades et poser des questions sur cet exercice en classe mais il ne sera pas donné de correction complète.
Exercice
Déterminer la gamme de distance focale que peut prendre le cristallin d’un oeil emmétrope.
TD Optique 3: L’oeil¶
Ces exercices seront traités en classe.
L’oeil et ses défauts¶
On désire étudier l’oeil et l’un de ses défauts: la myopie. On modélise l’oeil par une lentille convergente représentant le cristallin (distance focale image \(f'\), centre optique O) qui doit former l’image de l’objet observé sur la rétine qu’on modélisera par un écran situé en \(A'\) à une distance \(e=\overline{OA'}=15\rm{mm}\). L’oeil observe un objet situé en A à une distance \(\overline{AO}=d\).
Exercice
Rappeler la définition du Punctum Proximum (noté ici \(P_P\)) et du Punctum Remotum (noté ici \(P_R\)). On note \(d_m=\overline{P_P O}\) et \(D_m=\overline{P_R O}\) leur position respective (en valeur absolue) sur l’axe optique de l’oeil. Donner leur valeur pour un oeil normal (dit emmétrope), on note la valeur de \(d_m\) pour l’oeil emmétrope \(d_{m0}\).
On note \(V\) la vergence d’un cristallin pour un oeil emmétrope. \(V\) est une fonction de \(d\). Déterminer \(V(d)\). Montrer que la vergence augmente quand l’objet est de plus en plus proche.
Déterminer \(V(D_{m0})\) et \(V(d_{m0})\). L’oeil est au repos quand il observe un objet dans le plan du Punctum Remotum, la valeur \(V(D_{m0})\) est donc la vergence du cristallin quand l’oeil est au repos.
On suppose un oeil myope où le cristallin est trop convergent (cas de myopie assez rares). On note sa vergence \(V_m\). Celle-ci peut varier entre deux valeurs extrêmes qui sont: \(V(d_{m0})+\delta V\) et \(V(D_{m0})+\delta V\) avec \(\delta V > 0\) et constant quelque soit la position d de l’objet observé. On appelle \(\delta_V\) le degré de myopie.
Exercice
Un oeil myope et un oeil emmétrope observent tous deux un objet situé à une distance d (pour les deux yeux) de sorte que les deux yeux voient l’objet net. Quelle est la différence de vergence entre les deux cristallin?
Déterminer en fonction de \(d_{m0}\) et \(\delta V\), la position du \(P_P\) (notée \(d_{mm}\)) et du \(P_R\) (notée \(D_{mm}\)) pour un oeil myope. Justifier qu’on dise que le degré de myopie est l’inverse de la distance du Punctum Remotum.
Calculer leur position pour \(\delta V=0.1\delta; \delta V=4\delta; \delta V=10\delta\). Commenter.
On désire corriger un oeil myope grâce à une lentille de contact qu’on accole au cristallin (en première approximation). Quel est le type de lentille qu’on doit choisir et quelle est sa vergence?
On désire corriger un oeil myope grâce à un verre de lunette qu’on considère être une lentille de vergence \(V'\) dont le centre optique O’ est situé à \(d_L=\overline{O'O}=2\rm{cm}\)
Exercice
Déterminer la valeur de \(V'\) en fonction de \(\delta V\) et \(d_L\) pour que l’oeil myope puisse alors observer un objet à l’infini net tout en étant au repos. A.N. \(\delta V=4\delta\)
Par abus de langage, on appelle degré de myopie la vergence du verre correcteur (en valeur absolue) qu’il faut mettre devant un oeil pour corriger sa myopie. A quelle condition sur \(\delta V\) et \(d_L\), cette abus est-il acceptable?
Dans le cas où \(\delta V=4\delta\), calculer la nouvelle position du \(P_P\), on notera cette distance (dans le sens positif) \(d_{mc}\). Que devient cette distance dans le cas où \(\delta V \ll 1/d_L\)?