Exemples d’études¶
La correction de ces exercices méthodes est en ligne.
Lentille convergente¶
Exercice
On considère une lentille convergente de distance focale image f’. Déterminer le deux points sur l’axe optique H et H’ tels qu’un objet dans le plan frontal de H a une image dans le plan frontal de H’ et tel que le grandissement soit égale (algébriquement) à -1
Réaliser alors le tracé graphique.
Méthode
On a deux inconnues: les positions de H et H’ (qu’on pourra quantifier par des distances algébriques comme \(\overline{OH}, \overline{OH'}\) ou \(\overline{FH}, \overline{F'H'}\)).
Il nous faut donc deux équations:
la condition sur le grandissement.
la relation de conjugaison - il faudra en choisir une en fonction de ce qu’on veut trouver. On va ici déterminer les distances au centre optique, on utilisera la relation de Descartes.
Relation de conjugaison:
(11)¶\[\begin{equation} \frac{1}{\overline{OH'}} - \frac{1}{\overline{OH}} = \frac{1}{f'} \end{equation}\]Relation de grandissement:
(12)¶\[\begin{equation} \frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{OH'}}{\overline{OH}} = -1 \Longrightarrow \overline{OH'} = - \overline{OH} \end{equation}\]Il suffit de remplacer \(\overline{OH'}\) dans la relation de conjugaison
Tracé graphique
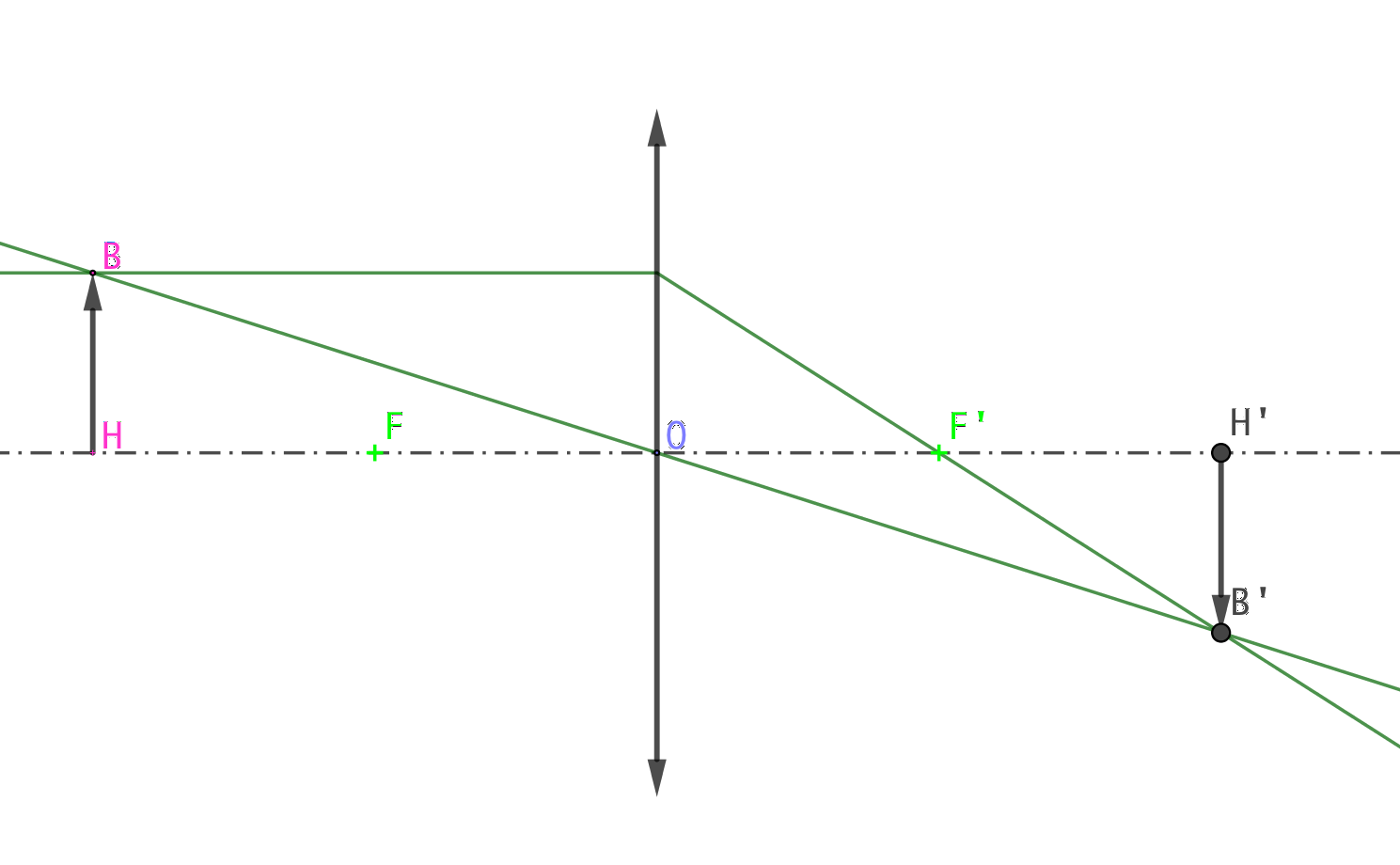
On commence par placer un point B dans le plan frontal de H et on chercher son image en traçant deux rayons: le rayon passant par B et le centre optique qui ressort non dévié et le rayon passant par B et parallèle à l’axe optique qui ressort en passant par le foyer principal image. Leur intersection permet de déterminer B’ et la projection de B’ sur l’axe optique donne H’.
Lentille divergente¶
Exercice
On considère une lentille divergente de distance focale image f’= - 10cm et un objet AB de taille h = 2cm (A est sur l’axe optique) situé à d = 20cm en amont du foyer principal objet.
Déteminer graphiquement puis numériquement la position et la taille de l’image A’B’ de AB par la lentille.
Correction - Graphique
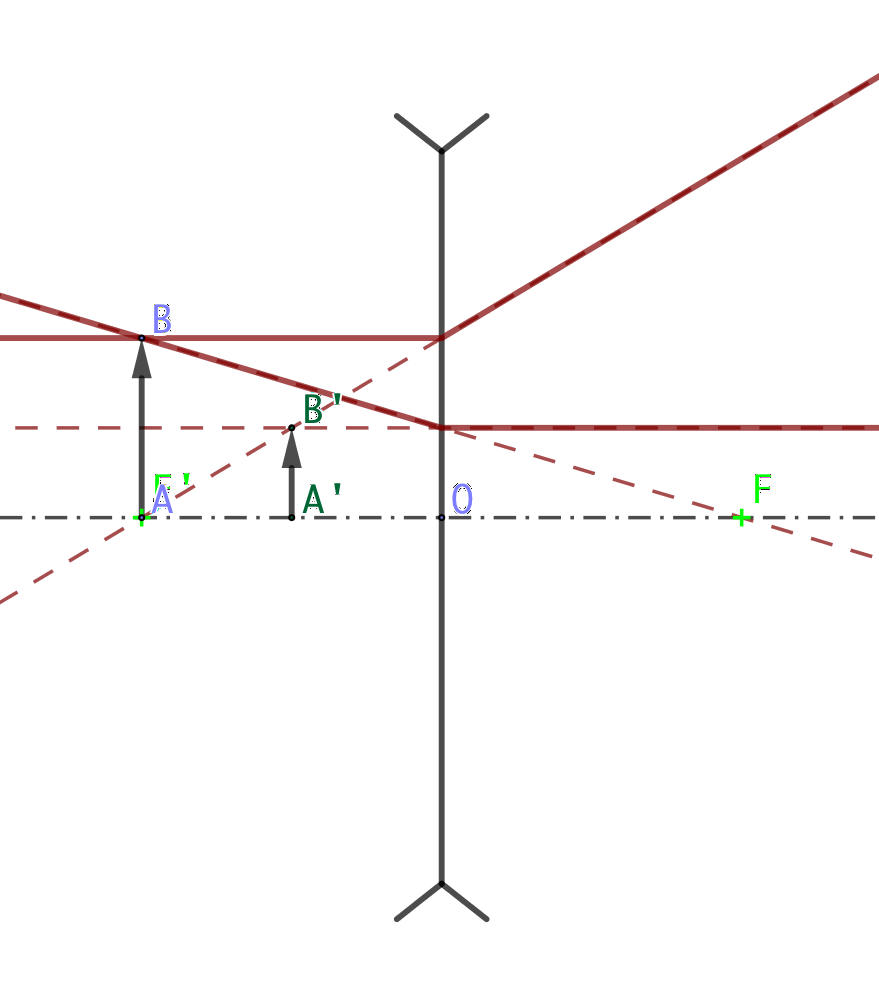
On utilise ce qui a été vu précédemment pour trouver la position de B’. Attention, le foyer principal image est AVANT la lentille et le foyer principal objet APRES la lentille.
On trace ici un rayon parallèle à l’axe optique passant par B, il ressort de la lentille en semblant provenir de du foyer principal image F’ (prolongement en pointillé).
On trace aussi un rayon passant par B et pointant vers le foyer principal objet F (partie en pointillé). Il ressort parallèle à l’axe optique.
On observe que le faisceau sortant diverge: le point de concours du faisceau doit donc être cherché dans le prolongement des rayons soit avant la lentille. L’image sera donc virtuelle. On trouve ainsi B’ puis A’ par projection.
Tip
Remarque Tracé des rayons virtuels.
Il est important de faire attention à la position des foyers et à l’utilisation des prolongement de rayons. Ainsi, on prolonge bien le rayon pour qu’il passe par F (rayon entrant) ou par F’ (rayon sortant).
De même, la divergence du faisceau sortant doit vous faire penser à utiliser leur prolongement pour chercher une image virtuelle.
Dans tout l’exercice, on remarquera que les rayons entrants (ou leur prolongement) doivent passer par le point B objet (puisqu’on cherche l’image de B… ).
Correction - Analytique
On va maintenant utiliser les relations de conjugaison pour déterminer la position de l’image puis une relation de grandissement pour déterminer sa taille.
Choix de la relation de conjugaison: la grandeur connue est la distance objet-foyer principal objet (ici \(\overline{FA} = - d\)). Donc on va plutôt utiliser la relation de Newton et chercher la distance \(\overline{F'A'}\).
On a donc:
(14)¶\[\begin{equation} \overline{FA} \cdot \overline{F'A'} = - f'^2 \Longrightarrow \boxed{\overline{F'A'} = \frac{f'^2}{d} = 5\rm{cm}} \end{equation}\]Il reste à utiliser une relation de grandissement (ici celle faisant intervenir \(\overline{FA}\)):
(15)¶\[\begin{equation} \frac{\overline{A'B'}}{\overline{AB}} = \frac{f'}{\overline{FA}} \Longrightarrow \boxed{\overline{A'B'} = - \frac{f'}{d}\overline{AB} = 1 \rm{cm}} \end{equation}\]
Hint
Vérification des résultats. On pensera à vérifier:
Homogénéité: On a à chaque fois une distance au carré sur une distance. Le résultat est bien homogène.
Cohérence entre le graphique et les expressions: Les résultats numériques sont cohérents puisque la distance OA’ et bien la moitié de OA (de même que pour les tailles) et A’ est bien une image virtuelle.
Position de l’image: Si l’on se réfère à une étude des zones d’espace conjuguée, on attendait bien une image virtuelle entre le foyer image et le centre optique puisque l’objet est réel et la lentille divergente.