Stigmatisme approché et condition de Gauss¶
Comme nous l’avons précisé précédemment, seul le miroir plan permet de réaliser un stigmatisme rigoureux. Mais on utilise pourtant des miroirs sphériques, des lentilles… Et l’on arrive à voir des images nettes.
Pour ce faire, on doit se placer dans un cadre moins “rigoureux” mais suffisant à cause des “imperfections” de notre oeil: le stigmatisme approché.
Stigmatisme approché¶
Absence de stigmatisme rigoureux (en ligne)¶
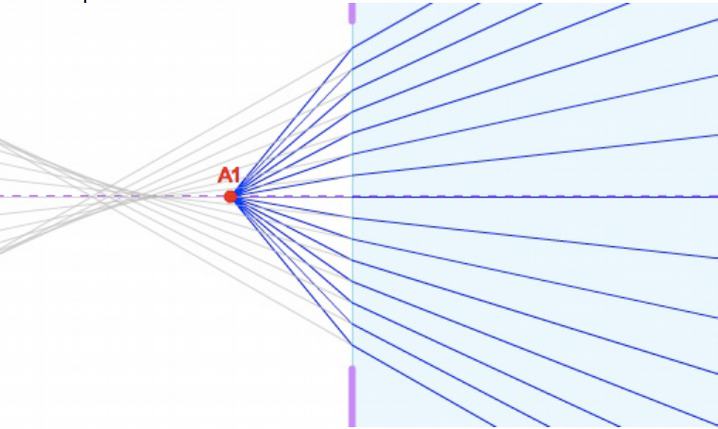
Absence de stigmatisme: Cas du dioptre plan
On observe sur la simulation suivante où le faisceau issu du point \(A_1\) ressort sans converger en un point précis. Il n’y a donc pas stigmatisme rigoureux.
Nous verrons sur des simulations ultérieures que le miroir sphérique ne réalise pas non plus de stigmatisme rigoureux.
Se rapproché du stigmatisme
Si l’on ne peut réaliser un stigmatisme rigoureux, on peut essayer s’en rapprocher en sélectionnant certains rayons qui passent tous à peu près en un même point.
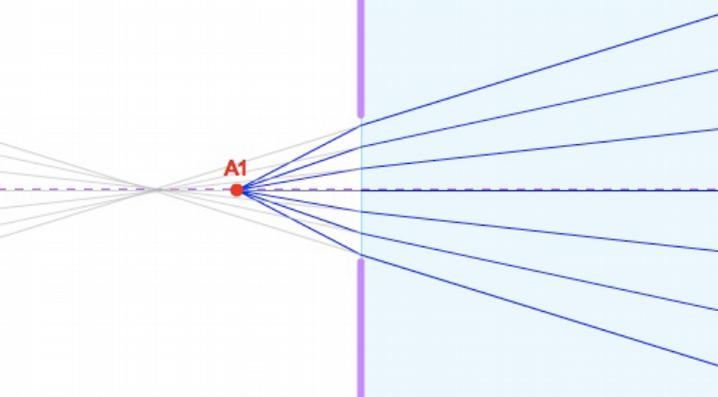
On peut le voir sur le cas du dioptre sur le schéma suivant. On a uniquement gardé les rayons peu inclinés et on peut considérer en première approximation qu’ils convergent en un point. Plus précisément en une tâche suffisamment petite pour que notre oeil ne puisse la distinguer d’un point.
C’est en sélectionnant les rayons qu’on pourra s’approcher du stigmatisme et donc réaliser… un stigmatisme approché.
Stigmatisme approché: sélection des rayons¶
Important
On dit qu’un système réalise un stigmatisme approché pour un couple de points (A;A’) si tous les rayons lumineux du faisceau issu du point A et traversant le système optique ressortent au voisinage du point A’.
A’ sera considéré comme l’image de l’objet A par le système optique et on dira que A’ et A sont conjugués.
Conditions de Gauss¶
Condition de Gauss: Simulation¶
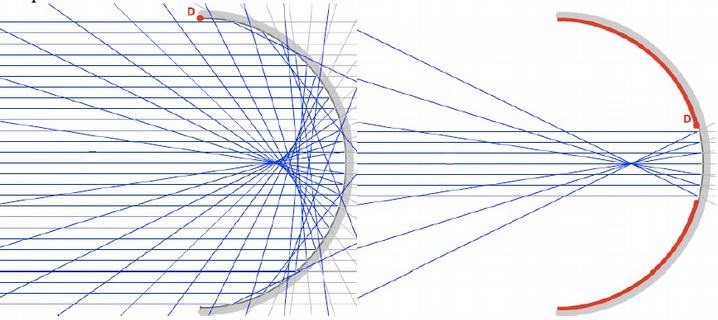
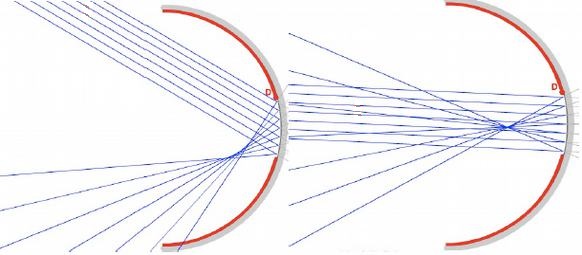
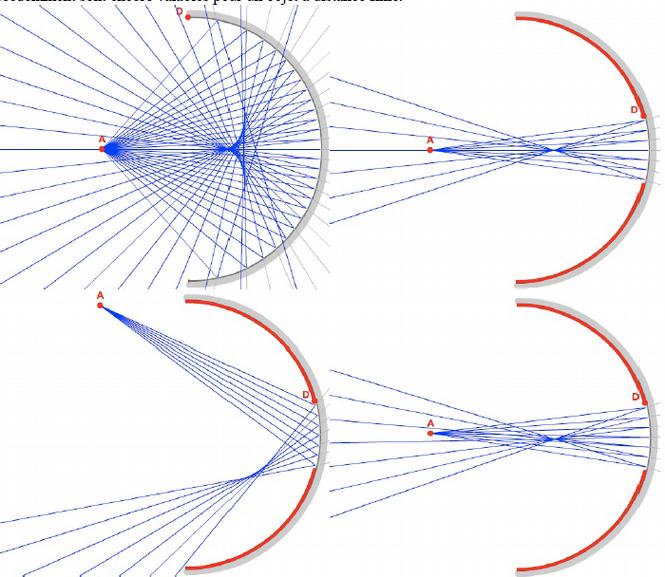
On utilisera ici un miroir sphérique pour réaliser la simulation du tracé des rayons. On utilise un point objet à l’infini dans un premier temps puis une simulation sur un objet à distance finie sera produite.
Condition de Gauss: Présentation¶
Important
Les conditions de Gauss (ou condition des rayons paraxiaux) sont un cadre théorique et expérimental dans lequel on sélectionne uniquement les rayons sont satisfont aux deux conditions:
ils ne doivent pas être trop inclinés par rapport à l’axe optique.
ils doivent entrer dans le système optique en un point proche de l’axe optique.
Un système centré placé dans les conditions de Gauss réalise un stigmatisme approché.
Complément : Aplanétisme (HP)
Il n’est pas nécessaire de le retenir mais se placer dans les conditions de Gauss permet aussi de réaliser un aplanétisme approché.
Conditions de Gauss: Réalisation expérimentale¶
En pratique, on va réaliser les conditions de Gauss en:
mettant un diaphragme en amont du système optique pour empêcher les rayons trop éloignés d’entrer.
mettant un diaphragme en aval du système optique (ou à l’intérieur) pour couper le passage des rayons trop inclinés.
Condition de Gauss: Utilisation analytique¶
Important
Approximations aux petits angles Dans le cadre des conditions de Gauss, il vient que les angles avec l’axe optique sont petits. On utilisera alors l’approximation des petites angles sur les fonctions trigonométriques:
Condition de Gauss: Aberrations¶
Si les conditions de Gauss ne sont pas respectées expérimentalement, cela donne lieu à des aberrations géométriques, c’est-à-dire que l’image sera déformée ou floue.