Systèmes centrées: présentation générales¶
Systèmes centrées: définition¶
Important
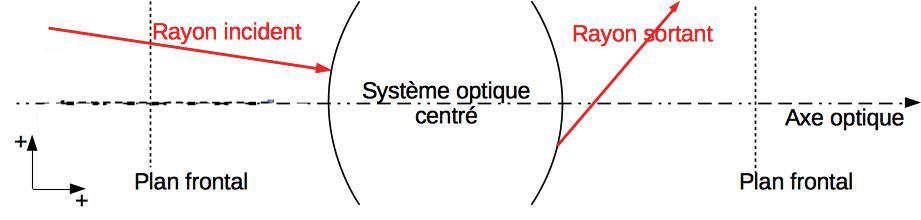
Un système centré est un système optique - c’est-à-dire une série de dioptre (et de surfaces réfléchissantes) - possédant un axe de révolution.
L’axe de révolution d’un système optique centré est appelé axe optique.
Tout plan perpendiculaire à l’axe optique est appelé plan frontal.
Rayons entrants et sortants¶
Important
Les rayons qui arrivent sur le système optique sont appelés rayons entrants ou rayons incidents.
La portion réellement parcourue par le rayon est appelé rayon réel. Son prolongement est appelé rayon virtuel.
Les rayons qui sortent du système optique sont appelés rayons sortants ou rayons transmis.
La portion réellement parcourue par le rayon est appelé rayon réel. Son prolongement est appelé rayon virtuel.

Objets réels et virtuels¶
Important
Définition : Objet ponctuel Lorsque les rayons entrants concourent en un point, on appelle ce point, point objet (ou objet).
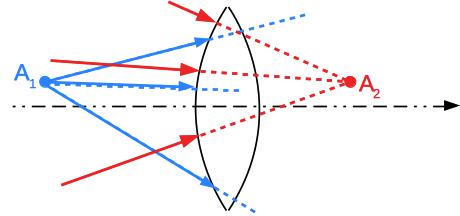
Si le point objet est le concours des rayons réels, alors on dit que l’objet est réel (comme \(A_1\) sur la figure ci-dessous).
Si le point objet est le concours du prolongements des rayons réels (rayons virtuels), on dit que l’objet est virtuel (comme \(A_2\)). Un objet virtuel est nécessairement formé par un système optique en amont.
Repérage d’un objet
On repérera un point objet par:
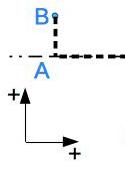
sa position longitudinale, c’est-à-dire la position du plan frontal où se trouve le point objet sur l’axe optique (donc la position du point A sur le graphique). L’axe optique est orienté et les distance sont algébriques (notée \(\overline{OA}\)).
sa position transversale, c’est-à-dire l’écart à l’axe optique. A nouveau, on travaille sur un axe orienté perpendiculaire à l’axe optique (on rappelle que la symétrie axiale permet de travailler sur un seul axe du plan frontal). Les positions sont donc algébriques (notée \(\overline{AB}\)).
Attention
Nature de l’objet
Un objet n’est pas nécessairement matériel (source primaire ou secondaire), il peut être aussi formé au concours de rayons transmis par un premier système optique (on dira qu’il est l’image - cf. suite - donnée par le premier système optique) avant d’entrée dans le second système optique (dont il est donc l’objet).
Exemple: Un oeil humaine utilise un télescope. Le téléscope vise une étoile (qui est un objet pour le téléscope) et en donne une image (grossie normalement). C’est cette image qui est vue par l’oeil. Elle est donc l’objet pour système optique {oeil} (plus exactement le cristalin).