Eléments principaux des systèmes centrés¶
Eléments principaux: foyers¶
Important
Foyers principaux objets et images
On définit le foyer principal objet comme le point où tout rayon incident passant par le foyer principal objet ressort du système optique (rayon transmis) en étant parallèle à l’axe optique.
Le foyer principal objet est donc l’antécédent du point à l’infini sur l’axe optique.
On définit le foyer principal image comme le point tel que tout rayon incident parallèle à l’axe optique ressort du système optique (rayon transmis) en passant par le foyer principal image.
Le foyer principal image est donc l’image du point à l’infini sur l’axe optique.
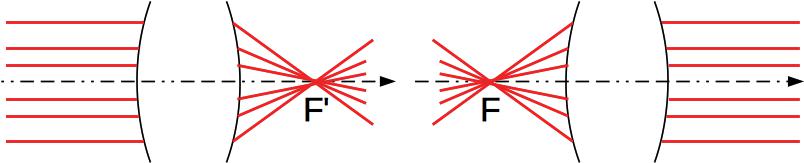
Fig. 10 Foyer principal image (gauche) et objet (droite)¶
Les plans focaux objet et image sont respectivement les plans frontaux contenant les foyers principaux objet ou image.
Important
Foyers secondaires objets et images, dropdown Les foyers secondaires objet et image sont les points respectivement du plan focal objet ou image n’étant pas sur l’axe optique.
Un foyer secondaire objet a pour image un point à l’infini hors de l’axe optique (qu’on peut représenter par un faisceau sortant parallèle entre eux mais non parallèle à l’axe optique). Une telle image est caractérisée par l’angle du faisceau ainsi formé.
Un foyer secondaire image a pour antécédent un point à l’infini hors de l’axe optique (qu’on peut représenter par un faisceau entrant parallèle entre eux mais non parallèle à l’axe optique). Un tel objet est caractérisé par l’angle du faisceau ainsi formé.
Eléments principaux: Centre optique et distance focale¶
Important
Centre optique Le centre optique est le point de l’axe optique où tout rayon incident pointant vers ce point ressort sans être dévié.
Important
Distance focale objet et image
Lorsque le centre optique existe, on définit la distance focale objet f comme la distance algébrique entre le centre optique O et le foyer principal objet F: \(f = \overline{OF}\)
Lorsque le centre optique existe, on définit la distance focale image f’ comme la distance algébrique entre le centre optique O et le foyer principal image F’: \(f' = \overline{OF'}\)
On définit la vergence \(V = 1 / f'\) avec \(f'\) la distance focale image. Son unité est la dioptrie notée \(\delta\)
Exemple: Détermination du foyer image d’un miroir sphérique.¶
Exercice
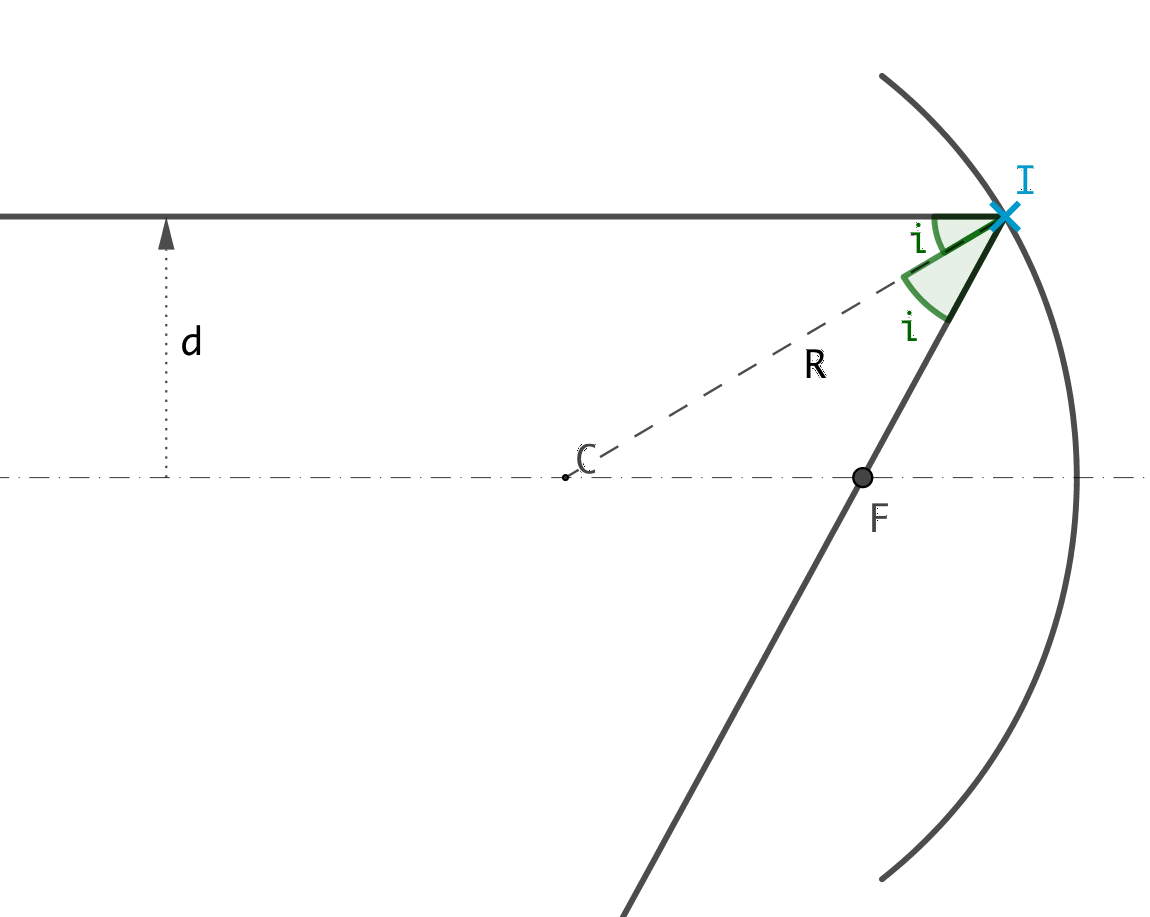
On considère une portion de sphère de rayon R dont l’intérieur est entièrement réfléchissant.
On considère un rayon incident parallèle à l’axe optique à une distance d de ce dernier. Représenter graphiquement le rayon réfléchi et l’intersection entre ce rayon et l’axe optique. Comment appellerait-on ce point ?
Déterminer la distance (algébrique) entre le centre de la sphère miroir et le point d’intersection précédent.
Simplifier l’expression précédente pour d >> R. Commenter le résultat.
La correction est en ligne.
Correction
Q1. On utilise l’égalité de l’angle incident et de l’angle réfléchie (la normale à une sphère est son rayon).
Le point F est le point d’intersection de rayons sortant issus des rayons incidents parallèle à l’axe optique, il correspond donc à un bon candidat pour le foyer principal image.
Q2. Le rayon incident est parallèle à l’axe optique, il vient que l’angle entre le rayon CI et l’axe optique est aussi l’angle i et le triangle CIF est donc isocèle en F.
On peut alors utiliser le produit scalaire:\[\begin{align*} CI^2 &= \overrightarrow{CI} \cdot \overrightarrow{CI} = \left(\overrightarrow{CF} + \overrightarrow{FI}\right) \cdot \left(\overrightarrow{CF} + \overrightarrow{FI}\right) \\ &= CF^2 + IF^2 + 2 \overrightarrow{CF} \cdot \overrightarrow{FI} = 2 CF^2 + 2 CF^2 \cos {\left(\pi - (\pi - 2i) \right)} \\ &= 2 CF^2 \left(1 + \cos 2i\right) \end{align*}\]Il vient:
(6)¶\[\begin{equation} \boxed{CF = \frac{R}{2 \cos i}} \end{equation}\]Remarque: On observe que la position du point dépend de l’angle et donc du rayon: on n’a pas de stigmatisme rigoureux.
Q3. Condition de Gauss. Lorsque \(d \ll R\), il vient que \(i \ll 1\) donc \(CF \approx \frac{R}{2}\)
Cette fois, la position du foyer ne dépend plus des rayons: en sélectionant les rayons paraxiaux (conditions de Gauss), on réalise un stigmatisme approché.
A retenir
L’utilisation de la géométrie et de la trigonométrie pour établir de relations mathématiques
L’utilisation des petits angles pour se placer dans les conditions de gauss
Dans les conditions de Gauss (ordre 1), on trouve normalement un résultat dépendant de la position de l’objet/image mais pas du rayon choisi (ici de l’angle i). C’est le stigmatisme approchée.