Sources d’incertitudes et bilan.
Contents
Dans ce notebook vous allez apprendre à faire un bilan des sources d’incertitude et à associer à chaque source une distribution statistique.
Sources d’incertitudes et bilan.#
Faire un bilan des sources#
Pour rappel, pour un mesurande directe il faut :
identifier ces facteurs (ces sources d’incertitudes)
associer à chaque source d’incertitude une distribution statistique et un écart-type.
combiner ces sources pour obtenir l’incertitude-type sur le mesurande étudié.
Attention
Attention, une source d’incertitude ne correspond pas à une grandeur d’influence mais à une contrainte pratique qui augmente la dispersion des résultats de mesurage. Une source d’incertitude est liée à une grandeur mesurée.
Danger
IL FAUT REFLECHIR ET NE PAS APPLIQUER DES RECETTES DE CUISINE SANS LES COMPRENDRE.
Sources usuelles#
Limitation de la précision de la mesure.#
C’est la principale source d’incertitude que nous allons rencontré. En effet, généralement lors d’une mesure, les limitations de l’instrument, le flou (en optique) et la variation de la grandeur mesurée fera qu’on ne pourra pas dire mieux que : le résultat de mesure se trouve dans tel intervalle.
Exemple : la mesure à la règle d’une position (ici les traits noir et vert)

Fig. 4 Mesure avec une règle#
Pour le trait noir (fin), la détermination de sa position est limitée par les graduations de la règle.
On peut dire que la mesure est entre \([3.7 cm; 3.8cm]\).
On choisira donc une distribution uniforme (toutes les valeurs 3.7 et 3.8 cm semblent possible de manière égale) d’intervale \([3.7 cm; 3.8cm]\).
L’incertitude-type sera \(1 / \sqrt{12} = 0.29 cm\)
Pour le trait vert (épais), on n’a plus un trait entre deux valeurs (cas d’une image un peu floue en optique).
On peut simplement dire que la mesure est entre \([4.4 cm; 4.7cm]\) (on ne limite par contre aux graduations car l’instrument ne permet pas mieux).
On choisira donc une distribution uniforme (toutes les valeurs 4.4 et 4.7 cm semblent possible de manière égale) d’intervale \([4.4 cm; 4.7cm]\).
L’incertitude-type sera \(3 / \sqrt{12} = 0.87 cm\)
Exemple : La fluctuation d’un appareil
On considère la mesure d’une tension \(U\) au moyen d’un multimètre numérique. Mais l’affichage fluctue et on observe que la mesure varie entre deux valeurs extrêmes : 2.43 V et 2.48 V.
On va donc choisire une distribution uniforme d’intervale \([2.43 V; 2.48 V]\).
L’incertitude-type sera \(0.05 / \sqrt{12} = 0.014 V\) (cf. suite).
Données d’un constructeur#
On est souvent amené à utiliser les données d’un constructeur pour estimer une incertitude.
Exemples
On utilise une lentille mince en optique de distance focale \(f' = 10 cm\), le constructeur nous dit que sa distance focale est connue à 10%.
Sans plus d’informations, on considèrera qu’il s’agit de l’incertitude-type associée à une distribution uniforme. On va donc associer à la valeur f’ une incertitude de distribution uniforme centrée en \(10 cm\) et de demie-largeur \(\frac{10}{100} \times 10 = 1 cm\).
Le multimètre numérique utilisé précédemment pour la mesure de U (dont la valeur mesurée est donc \(\frac{2.43 + 2.48}{2} = 2.455 V\)) est sujet à une dispersion des valeurs données, même si l’affichage est stable. Ainsi, le constructeur nous dit que la valeur mesurée, sur le calibre utilisé, possède une incertitude de 2%.
A nouveau peu d’information, on va à nouveau considérer une distribution uniforme centrée sur 2.455 V et de demie-largeur \(\frac{2}{100} \times 2.455 = 0.049 V\).
Combiner plusieurs sources d’incertitude#
Il arrive fréquemment qu’il existe plusieurs sources d’incertitudes pour un même mesurande.
Méthodes
Pour estimer l’incertitude-type totale sur le mesurande \(U\), on dispose de deux méthodes :
On simule les processus aléatoires de chaque sources d’incertitude grâce aux distributions choisie un grand nombre de fois et on simule ainsi la variabilité du mesurande. On parle de simulation de Monte-Carlo.
On réalise une propagation des variances (application des propriétés de la variance mathématique sur des lois statistiques) ce qui nous donne l’incertitude-type (mais pas la distribution).
Simulation de Monte-Carlo.#
Principe#
Le principe est le suivant :
Pour chaque source d’incertitude indépendante, on a choisi une distribution statistique et son écart-type. On peut donc simuler la variabilité causée par chaque source en réalisant un tirage aléatoire de N échantillons suivant la loi statistique choisie centrée en 0.
On somme alors les différents tirages avec le résultat de mesurage ce qui nous donne la valeur simulée du mesurande soumise à la variabilité de TOUTES les sources.
On peut alors tracer l’histogramme des valeurs pour observer la distribution obtenus et calculer l’écart-type associé pour estimer l’incertitude-type totale.
Exemple
Dans le cas de la tension U, la procédure sera :
On simule N échantillons d’une distribution uniforme entre \(-0.014 V\) et \(0.014 V\) (simulation de l’incertitude liée à la lecture de la valeur).
On simule N échantillons d’une distribution gaussienne d’écart-type \(0.049 V\) centrée en 0 (simulation de l’incertitude liée à la variabilité de l’appareil de mesure).
On somme les échantillons des deux distributions et on ajoute la valeur mesurée (ici 2.455). On obtient ainsi N échantillons simulés de \(U\).
On étudie la distribution statistique ainsi obtenue et on déterminer l’incertitude-type sur U grâce à l’écart-type des N tirages.
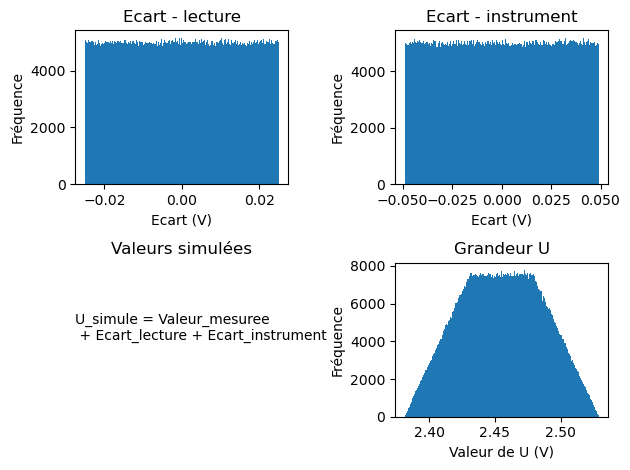
Fig. 5 Titre#
On obtient U = 2.455 \(\pm\) 0.032 V.
Propagation des variances#
Cette méthode sera présentée plus tard.
