Comparer un résultat expérimental avec un résultat théorique.
Contents
Obtenir une mesure n’est en général pas suffisant, il est important d’exploiter les résultats obtenus en vue de répondre à la problématique fixée. Vous aller apprendre ici à comparer un résultat expérimental à un résultat attendu (théorique, valeur constructeur…)
Comparer un résultat expérimental avec un résultat théorique.#
Comparaison qualitative.#
Une première étude peut-être réalisée en comparant les intervalles associées au couple {résultat de mesurage + incertitude de mesure} à la valeur théorique attendue. Si la barre d’incertitude comprend la valeur théorique, on peut considérer que la théorie et l’expérience sont compatibles.
Limites
Cette comparaison a ses limites car l’intervalle défini par l’écart-type autour du résultat de mesurage exclut des valeurs qui ont une probabilité encore importante d’être réalisée.
Dans le cas d’une distribution gaussienne, un valeur lors d’un tirage n’a que 63% de chance de se trouver dans l’intervalle à un écart-type. On ne tient pas compte d’un tiers des valeurs en raisonnant de cette façon.
Ecart-normalisé#
Important
Ecart normalisé
Pour tester la compatibilité entre une valeur attendue \(g_{att}\) d’incertitude \(u(g_{att})\) et un résultat de mesurage \(g_{mes}\) d’incertitude \(u(g_{mes})\), on calcule l’écart normalisé:
Si l’écart normalisé est inférieur à 2, on considérera que valeur attendue et expérience sont compatibles.
Si l’écart normalisé est supérieur à 2, on considérera que valeur attendue et expérience ne sont pas compatibles.
Explication du raisonnement. (en ligne)#
Explications
On considère :
qu’on étudie une grandeur G possèdant une valeur attendue \(G_{att}\) dont la valeur est \(g_{att}\) avec une incertitude \(u(G_{att})\). On supposera que la distribution suivie est une distribution gaussienne.
on a réalise le mesurage de la grandeur G (appelé \(G_{mes}\)) dont le résultat de mesurage est \(g_{mes}\) avec une incertitude \(u(G_{mes})\). On supposera aussi que la distribution est gaussienne.
On veut savoir si la valeur mesurée et la valeur attendue sont cohérentes. On espère avoir un écart nul \(g_{mes} - g_{att} = 0\) mais il est évident que ce n’est pas possible car les deux grandeurs sont soumises à une incertitude (variabilité ou manque d’information).
Par contre, la grandeur \(\Delta G = G_{mes} - G_{att}\) est aussi un mesurande qu’on peut voir comme une variable aléatoire. Et si valeur attendue et expérience sont cohérentes, alors on attend l’espérance de cette distribution soit 0 (distribution centrée).
De plus, \(G_{mes}\) et \(G_{att}\) étant indépendante, on peut connaître la variance de leur différence grâce aux théorèmes mathématiques sur la variance : \(v_{\Delta G} = v_{G_{mes}} + v_{G_{att}}\) soit pour les écart-type:
En divisant \(\Delta G\) par \(\sigma_{\Delta G}\), on aura donc une variable aléatoire \(\eta_G\) qui aura un écart-type égal à 1 (distribution réduite). Donc:
Si l’expérience et les attentes (théoriques ou constructeur) sont compatibles, on attend donc que la variable aléatoire associée au mesurande ;
\[ \eta_G = \frac{G_{mes} - G_{att}}{\sqrt{\sigma^2(G_{mes}) + \sigma^2(G_{att})}} \]soit une distribution centrée réduite.
On s’est donc ramené à l’idée que pour tester la compatibilité valeur attendue-expérience, il ne faut pas attendre un écart nul mais des données compatibles avec une estimation de \(\eta_G\). On rappelle qu’on ne possède pas l’allure de \(\eta_G\) mais uniquement \(g_{mes}, u(G_{mes}), g_{att}, u(G_{att})\), on ne peut donc qu’estimer \(\eta_G\) par:
Il faut donc un critère sur la valeur de \(\eta\) pour savoir s’il y a compatibilité ou non.
Il existe des tests en statistique permettant à partir d’une estimation de décider si l’hypothèse d’une distribution centrée réduite est acceptable ou non. Ces tests ne sont pas au programme, on admet que cela revient à fixer une valeur seuil pour \(\eta\) et considérer que si la valeur seuil est dépassée, il n’y a pas compatibilité. Si \(\eta\) est inférieure à cette valeur seuil, il y a compatibilité.
Dans le cadre des classes préparatoires, le choix de cette valeur seuil est fixé à 2. Cela revient, dans l’hypothèse d’une distribution gaussienne, à rejeter une compatibilité avec un risque d’erreur de 5%.
Exemples d’utilisation (en ligne)#
Résultat unique
On va reprendre l’exemple de l’étude d’une résistance électrique. Cela sera aussi l’occasion de comprendre graphiquement la notion d’écart normalisé. On ne refait pas toute l’étude. On supposera :
Cas 1 :
qu’on a mesuré une valeur de résistance \(R = 373,1 \pm 3,5 \Omega\)
que le constructeur donne une valeur de résistance : \(R = 370 \pm 4 \Omega\)
Cas 2 :
qu’on a mesuré une valeur de résistance \(R = 398,5 \pm 6,1 \Omega\)
que le constructeur donne une valeur de résistance : \(R = 370 \pm 4 \Omega\)
On obtient :
Cas 1 : \(\eta =\)0.6
On peut donc conclure que la valeur constructeur et l’expérience réalisée sont compatibles.
Cas 2 : \(\eta =\)3.9
On doit considérer que la valeur constructeur et l’expérience réalisée ne sont pas compatibles.
Il ne faut pas en rester là et chercher les causes de cette incompatibilité.
Analyse graphique
Puisqu’on possède les valeurs mesurées et les incertitudes, on va pouvoir faire une simulation de Monte-Carlo des grandeurs. On a réalisé N=1000000 simulations.
On représente ci-dessous (chaque ligne correspond à un cas) :
Les barres d’incertitudes pour la valeur expérimentales puis pour la valeur constructeur.
Les histogrammes des deux distributions (valeur expérimentale et valeur constructeur)
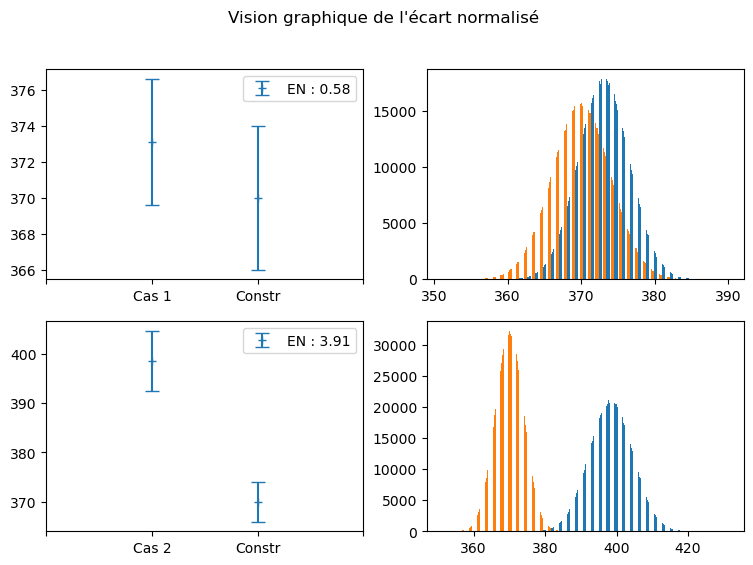
Multiples résultats#
On peut se servir de l’écart normalisé pour tester la compatibilité d’un ensemble de mesures entre elles. On se limite en général à calculer l’écart normalisé entre la moyenne et chaque résultat.
On peut aussi tester les écarts à un modèle (théorique ou calculé) sur plusieurs valeurs grâce à l’écart normalisé.
