Dans cette partie, vous allez apprendre à propager des incertitudes vers des mesurandes indirects.

Pour rappel un mesurande direct est obtenu par lecture sur un instrument de mesure alors qu’un mesurande indirect est obtenue par calcul à partir des mesurandes directs.

Cette fois, on ne peut évaluer des composantes de l’incertitude d’un mesurande indirect liés au processus de lecture du résultat de mesurage, puisqu’on le calcule.

Incertitude des mesurandes indirectes.

Position du problème.

On a mesuré des grandeurs \(X_i\) dont on a estimé l’incertitude-type (et la distibution statistique possiblement) et on considère un mesurande Y qu’on recherche et qu’on peut estimer grâce à une relation :

\[ Y = f(X_i) \]

On veut estimer l’incertitude-type sur Y et possiblement aussi sa distribution statistique.

Exemple

On veut mesurer la valeur \(R\) d’une résistance électrique. On a mesuré la tension \(U\) à ses bornes et l’intensité \(I\) qui la traverse. On va estimer la résistance en utilisant la loi d’Ohm : \(R = U / I\).

Méthodes

Il existe deux méthodes :

1. La simulation de Monte-Carlo. Le principe est exactement le même que précédemment. La différence est qu’on a plus besoin de centrer les distributions des \(X_i\) autour de 0.

2. La propagation des variances. On utilise des relations entre les variances de grandeurs liés entre elles.

Attention

Dans les deux cas, on est obligé de supposer que les mesurandes \(X_i\) sont tous indépendants. Sinon, les deux méthodes ne sont pas valables.

Simulation de Monte-Carlo.

Rappel

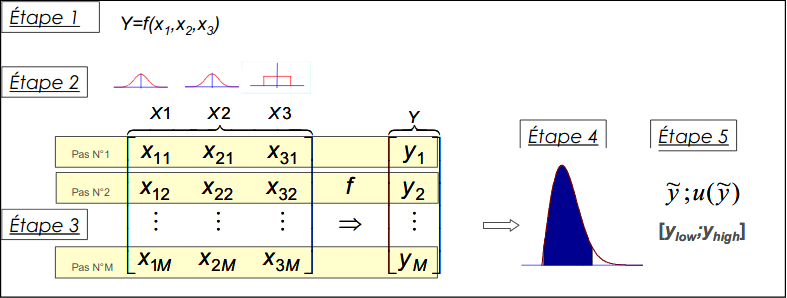
On rappelle brièvement le principe de la simulation de Monte-Carlo. On connaît la distribution statistique de chaque mesurande \(X_i\). On va simuler N échantillons de chaque \(X_i\) puis on calcule ainsi N échantillons \(Y\). On obtient ainsi la distribution des valeurs de \(Y\) et on peut calculer son incertitude de mesure.

Exemple

On a supposé pour simplifier que les incertitude-type et distribution des mesurandes directs ont déjà été déterminées. En pratique, elles sont souvent déterminées à partir d’une ou plusieurs sources d’incertitudes. On peut alors combiner la méthode présentée précédemment et celle présentée ici.

Résistance électrique

On reprend l’exemple précédent de l’estimation de l’incertitude de la résistance R. On a mesuré tension et intensité. On a trouvé :

• Un tension \(U = 4.53 V\) avec une incertitude \(u(U) = 0.03 V\). On a estimé que la loi de probabilité étant gaussienne.

• Une intensité \(I = 12.14 mA\) avec une incertitude \(u(I) = 0.08 mA\). On a estimé que la loi de probabilité étant gaussienne.

La méthode est :

1. On créer deux vecteurs de taille N contenant des tirages aléatoires de U et I basés sur les distibutions choisies.

2. On obtient un vecteur de taille N contenant des valeurs simulés de R.

3. On trace l’histogramme et on calcule la moyenne et l’écart-type de la distribution qui nous donnerons le résultat de mesurage et l’incertitude-type.

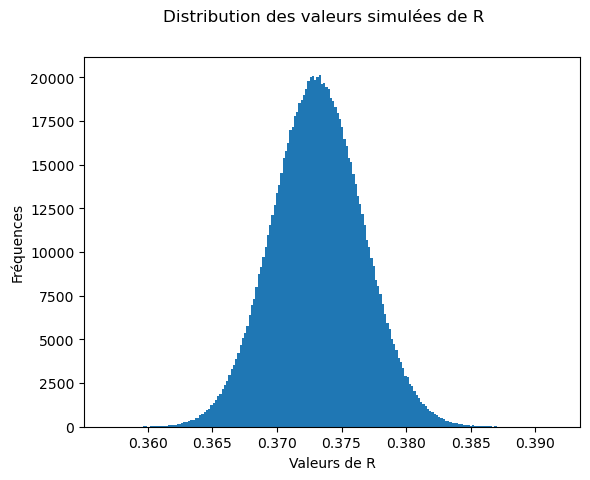
Fig. 6 Titre

On obtient R = 373.2 \(\pm\) 3.5 \(\Omega\).

Propagation des variances

Cette méthode sera présentée plus tard dans l’année.