Résolution d’équation stationnaire
Contents
2. Résolution d’équation stationnaire#
On va ici donner quelques méthodes pour résoudre une équation stationnaire, c’est-à-dire résoudre une équation du type:
sur un intervalle \([a,b]\) dans lequel on sait qu’il n’y a qu’une seule racine qui sera noté \(x_0\).
2.1. Unicité de la racine#
L’hypothèse d’unicité de la racine est fondamental car sinon, on ne sait pas si on va obtenir celle voulue. La résolution d’une équation stationnaire passe donc par une étude initiale de la fonction pour réduire l’intervalle de recherche à un intervalle ne contenant qu’une seule racine.
2.2. Méthode par dichotomie#
Condition: \(f\) est continue sur l’intervalle \([a,b]\) et \(f(a) f(b) < 0\) (ainsi \(f\) admet au moins une racine dansl’intervalle (TVI)).
Principe:
On coupe l’intervalle \([a,b]\) en deux parties égales (soit \(c = \frac{a+b}{2}\)) le milieu
On regarde dans quelle moitié se trouve la racine en testant les signes des produits \(f(a)f(c)\) et \(f(c)f(b)\)
Si \(f(a)f(c) < 0\), la racine est dans l’intervalle \([a,c]\), on réitère le test précédent mais avec l’intervalle \([a,c]\) (soit \(b = c\) maintenant)
Si \(f(c)f(b) < 0\), la racine est dans l’intervalle \([c,b]\), on réitère le test précédent mais avec l’intervalle \([c,b]\) (soit \(a = c\) maintenant)
On recommence jusqu’à atteindre un critère fixé:
soit la largeur de l’intervalle de recherche est plus petit que la précision choisie : \([a_{finale}, b_{finale}] < precx\)
soit le maximum de \(f\) sur l’intervalle \([a_{finale}, b_{finale}]\) est inférieure à une précision choisie \(precy\)
on peut imposer les deux conditions si nécessaire.
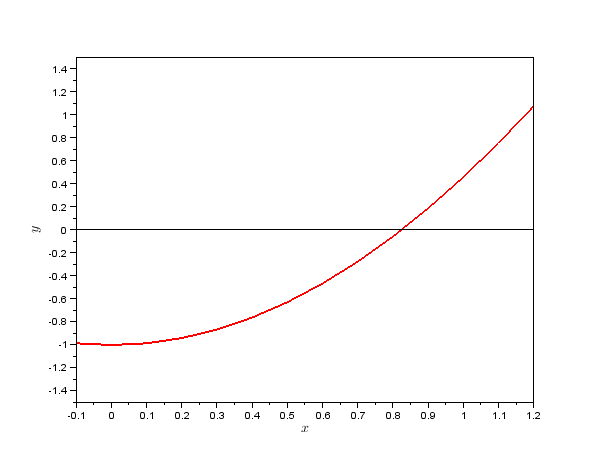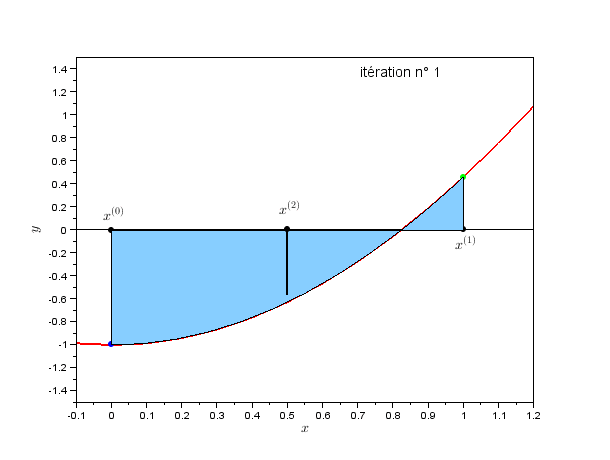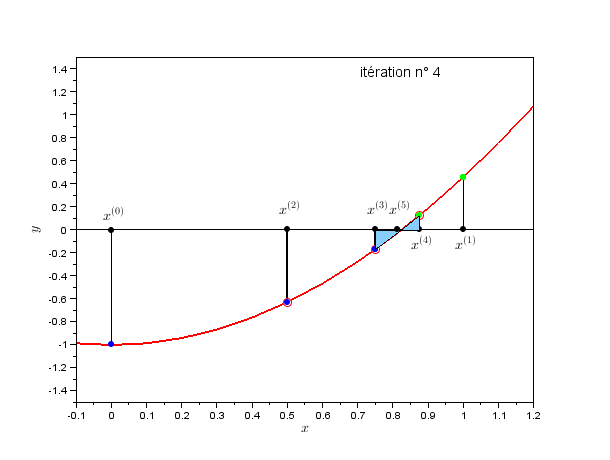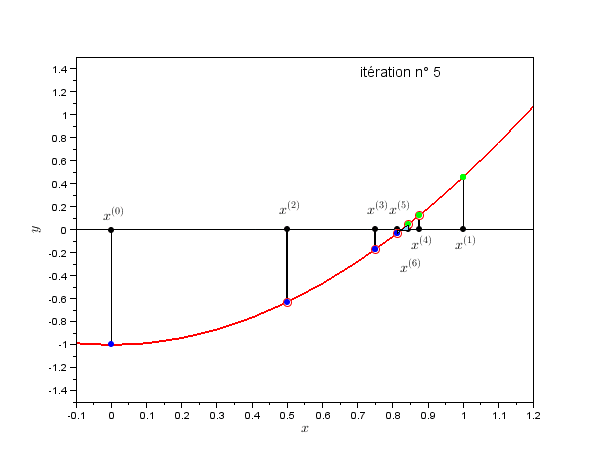
Fig. 2.1 Méthode par dichotomie#
2.3. Méthode de Newton#
Condition: \(f\) est de classe \(C^1\) sur l’intervalle \([a,b]\).
On part d’une valeur \(x_0\) dans l’intervalle et on trace la tangente à la courbe de \(f\) en \(a\). Son équation est:
On cherche alors l’abscisse \(x_1\) où la tangente coupe l’axe des abscisse soit:
On recommence en travaillant avec la tangente en \(x_1\)
On s’arrête quand un critère similaire à la dichotomie (écart entre deux abscisses \(x_{i+1}\) et \(x_i\) ou faible valeur de \(f(x_i)\)) est atteint.
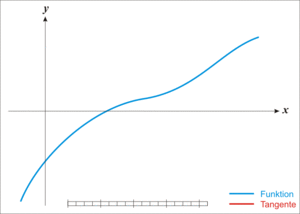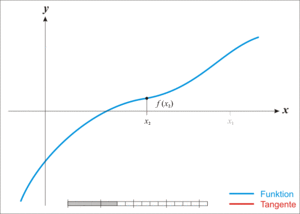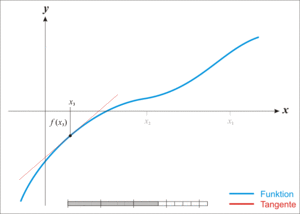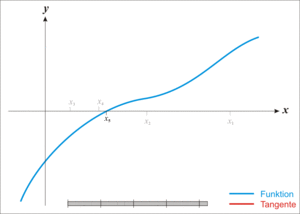
Fig. 2.2 Méthode par Newton#
Avantage et inconvénient: La méthode de Newton est beaucoup plus rapide que la méthode par dichotomie mais elle nécessite de connaître la dérivée ou de la calculer par dérivation numérique.

