2. Dérivation et intégration numérique

Les méthodes de dérivation et d’intégration numérique sont basées sur la définition même de ces concepts mais sans le passage à la limite.

2.1. Dérivation numérique.

2.1.1. Principe

Rappel : Soit une fonction \(f\) définie et dérivable en \(x_0\). Le nombre dérivée de \(f\) en \(x_0\) est:

\[ f'(x_0) = \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h}\]

L’idée de la dérivation numérique est d’approcher le nombre de dérivée \(f'(x_0)\) par le calcul du taux de variation précédent pour un un \(h\) non nul (on approxime donc géométriquement la tangente par la corde):

\[ f'(x_0) \approx \frac{f(x_0 + h) - f(x_0)}{h}\]

2.1.2. Types de calcul

On distingue trois façons de calcul un nombre dérivé:

Dérivée à droite

\[ f'(x_0) \approx \frac{f(x_0 + h) - f(x_0)}{h}\]

Dérivée à gauche

\[ f'(x_0) \approx \frac{f(x_0) - f(x_0 - h)}{h}\]

Dérivée centrée

\[ f'(x_0) \approx \frac{f(x_0 + h) - f(x_0 - h)}{2h}\]

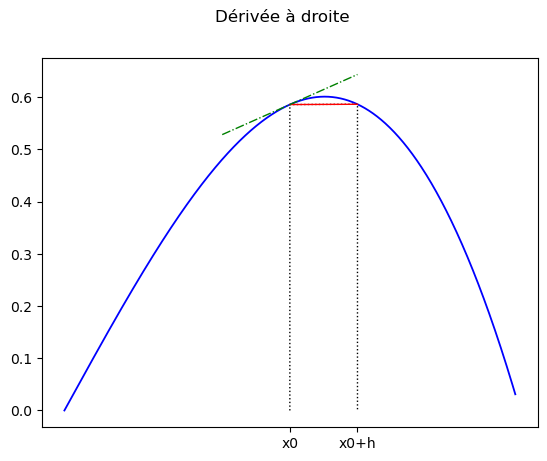
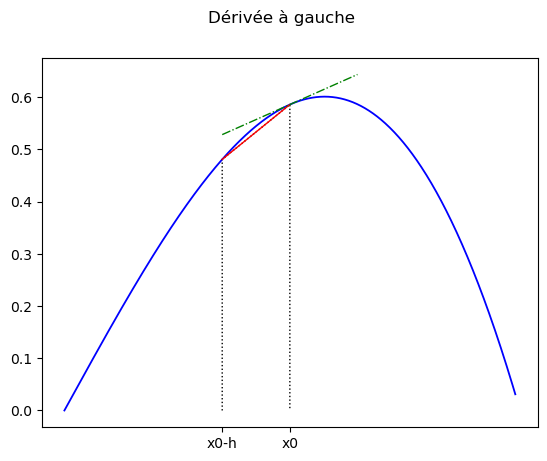
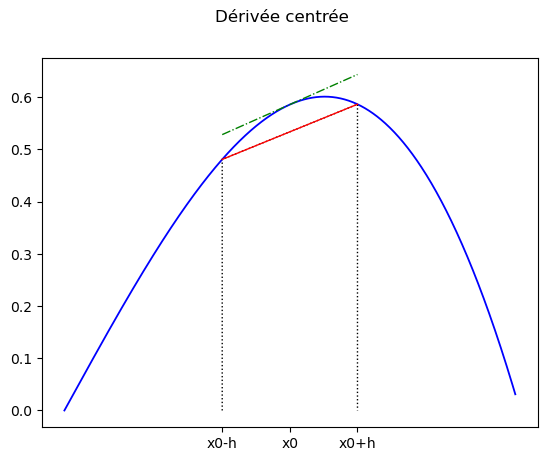
Fig. 2.1 Note : La dérivée centrée est en général plus précise.

2.1.3. Cas étudiés et pas de calcul

En général, on estime la fonction dérivée sur un intervale \([a,b]\), soit une estimation du nombre dérivée pour plusieurs valeurs \(x_i \in [a,b]\) avec un pas \(h\). On distingue deux cas:

• La fonction \(f\) est connue analytiquement mais on ne veut/peut pas faire le calcul analytique de la dérivée. On peut alors choisir les \(x_i\) et choisir le pas de dérivation comme on veut.

Cas des valeurs discrètes

C’est le cas en général lorsque les \(y_k\) sont issus d’une mesure expérimentale par exemple.

Note : Par manque d’information, le nombre dérivée en \(x_0\) ne peut alors être calculé que par dérivation à droite et le nombre dérivée en \(x_{N-1}\) (dernier échantillon) ne peut être calculé que par dérivation à gauche. Pour les autres, on a le choix.

• La fonction \(f\) n’est pas connue. On a juste les valeurs \(y_k = f(x_k)\) pour des abscisses \(x_k\) (k entier dans \([0;N-1]\)). On ne peut alors calculer la dérivée de \(f\) qu’aux points \(x_k\) et le pas d’intégration est nécessairement \(h = x_{k+1} - x_k\) (à adapter pour la dérivée à gauche et centrée).

2.2. Intégration numérique

2.2.1. Principe

Rappel : L’intégrale d’une fonction \(f\) sur l’intervalle \([a; b]\) est définie par:

\[I = \int_a^b f(x) dx = \lim_{N \to \infty} \sum_{i=0}^{N-1} f(x_i) \times h\]

avec \(x_i = a + \frac{b-a}{N}i\) et \(h = \frac{b-a}{N}\)

Relation de récurrence

Si l’on définit \(I_k = \sum_{i=0}^{k} f(x_i) \times h\), on remarque la relation de récurrence:

\[ I_{k+1} = I_k + f(x_{k+1}) \times h \]

et \(I \approx I_{N-1}\)

C’est une méthode très pratique pour calculer I par une boucle.

L’idée de l’intégration numérique est donc d’approcher le calcul intégrale en prenant une valeur finie pour \(N\), c’est-à-dire une valeur non nulle pour \(h\) :

\[ I \approx \sum_{i=0}^{N-1} f(x_i) \times h \]

2.2.2. Type d’intégration

On distingue quatre types d’intégration:

Méthode des rectangles à droite

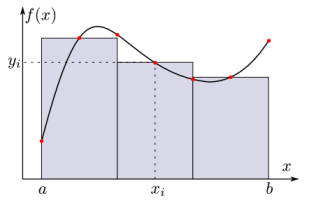
On commence à \(a\) et on s’arrête à \(b - h\). L’aire d’un rectangle est:

\[ \mathcal{A_i} = f(x_{i}) \times h \]

Méthode des rectangles à gauche

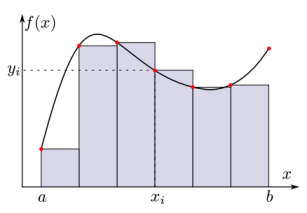
On commence à \(a + h\) et on s’arrête à \(b\). L’aire d’un rectangle est:

\[ \mathcal{A_i} = f(x_{i} + h) \times h \]

Méthode des rectangles centrés

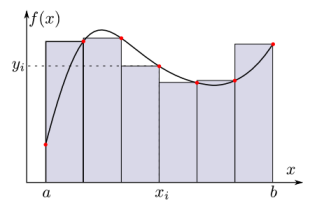
On commence à \(a + h / 2\) et on s’arrête à \(b - h / 2\). L’aire d’un rectangle est:

\[ \mathcal{A_i} = f(x_{i} + h /2) \times h \]

On peut aussi sauter une valeur sur deux comme sur la figure.

Méthode des trapèzes

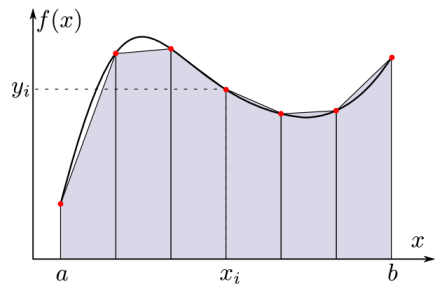
L’aire d’un trapèze est:

\[ \mathcal{A} = \frac{f(x_{i} + h) + f(x_i)}{2}h \]

2.2.3. Cas étudiés et pas de calcul

Comme pour la dérivation, on distingue deux cas:

• La fonction \(f\) est connue analytiquement mais on ne veut/peut pas faire le calcul analytique de l’intégrale. On peut alors choisir les \(x_i\) et choisir le pas d’intégration comme on veut (ou choisir N).

Cas discret

Il est possible que le pas \(h = x_{i+1} - x_i\) varie dans le cas de mesures. Ce n’est pas un problème.

• La fonction \(f\) n’est pas connue. On a juste les valeurs \(y_k = f(x_k)\) pour des abscisses \(x_k\) (k entier dans \([0;N-1]\)). Le pas \(h\) est alors imposée par les \(x_{i+1} - x_i\). On peut néanmoins toujours la méthode d’intégration.

Dans les deux cas, la méthode par récurrence est conseillée. D’autant qu’elle permet de calculer l’intégrale sur plusieurs intervalles \([x_0, x_k]\) (\(k \in [0, N-1]\)). La suite \(I_k\) ainsi obtenue donc une primitive (qui s’annule en \(x_0\)) de la fonction \(f\) sur l’intervalle étudiée.