La page ci-présente existe en version notebook téléchargeable grâce au bouton (choisir le format .ipynb). On rappelle qu’il faut ensuite l’enregistrer dans un répertoire adéquat sur votre ordinateur (capa_num par exemple dans votre répertoire personnel) puis lancer Jupyter Notebook depuis Anaconda pour accéder au notebook, le modifier et exécutez les cellules de code adéquates.

2.5. Exemple d’implémentation

2.5.1. Implémentation

On présente des exemples d’implémentation des différentes dérivations.

2.5.1.1. Dérivation numérique

from numpy import *
from matplotlib.pyplot import *

def d_g(f, x0, pas):
  """Dérivation à gauche"""
  return (f(x0) - f(x0 - pas)) / pas

def d_d(f, x0, pas):
  """Dérivation à gauche"""
  return (f(x0 + pas) - f(x0)) / pas

def d_c(f, x0, pas):
  """Dérivation à gauche"""
  return (f(x0 + pas) - f(x0 - pas)) / (2 * pas)

def d_discrete(xk, yk):
  """Dérivée discrète"""
  n = len(xk)
  dy = [(yk[1] - yk[0])/ (xk[1] - xk[0])]  # Premier terme - Dérivée à gauche
  for k in range(1, n - 1): # Pas le premier ni le dernier cas
    dy.append((yk[k+1] - yk[k-1])/ (xk[k+1] - xk[k-1]))  # Dérivée au centre
  dy.append((yk[n-1] - yk[n-2])/ (xk[n-1] - xk[n-2]))  # Dérivée à droite
  return array(dy) # transformation en vecteur numpy

2.5.1.2. Intégration numérique

from numpy import *
from matplotlib.pyplot import *

def i_g(f, x0, xf, N):
  """Intégration par rectangle à gauche"""
  I = 0
  pas = (xf - x0) / N
  for k in range(1,N+1): # On commence à 1 pour placer les rectangles à gauche
    I += f(x0 + k * pas) * pas
  return I

def i_d(f, x0, xf, N):
  """Intégration par rectangle à droite"""
  I = 0
  pas = (xf - x0) / N
  for k in range(0,N): # On commence à 0 pour placer les rectangles à droite
    I += f(x0 + k * pas) * pas
  return I

def i_c(f, x0, xf, N):
  """Intégration par rectangle au centre"""
  I = 0
  pas = (xf - x0) / N
  for k in range(0,N):
    I += f(x0 + (k + 1/2) * pas) * pas  # Décalage de 1/2 pour centrer les rectangles
  return I

def i_t(f, x0, xf, N):
  """Intégration par trapèzes"""
  I = 0
  pas = (xf - x0) / N
  for k in range(0,N):
    I += (f(x0 + k * pas) + f(x0 + (k+1) * pas)) / 2 * pas  # Aire d'un trapèze

def i_discrete(xk, yk):
  """Integration discrète"""
  n = len(xk)
  I = [0]  # Premier terme nul - intégrales toute à partir de x0
  for k in range(1, n): # Pas le premier terme
    I.append(I[-1] + (yk[k] + yk[k-1]) / 2 * (xk[k] - xk[k-1]))  # Trapèze - Suite de valeurs
  return array(I) #

2.6. Implémentation

from urllib.request import urlopen # Pas à connaître
url = "https://github.com/pcsi3physiquestan/donnees_exp/blob/main/circuit_rc.dat?raw=true"
webpage = urlopen(url)


datas = loadtxt(webpage, skiprows = 7, delimiter=";")
deriva = d_discrete(datas[:, 0], datas[:, 1])
integr = i_discrete(datas[:, 0], datas[:, 1])
f, ax = subplots(1, 3)
ax[0].set_title("Données")
ax[0].plot(datas[:, 0], datas[:, 1])
ax[1].set_title("Dérivée")
ax[1].plot(datas[:, 0], deriva)
ax[2].set_title("Primitive")
ax[2].plot(datas[:, 0], integr)

[<matplotlib.lines.Line2D at 0x209e76beb80>]

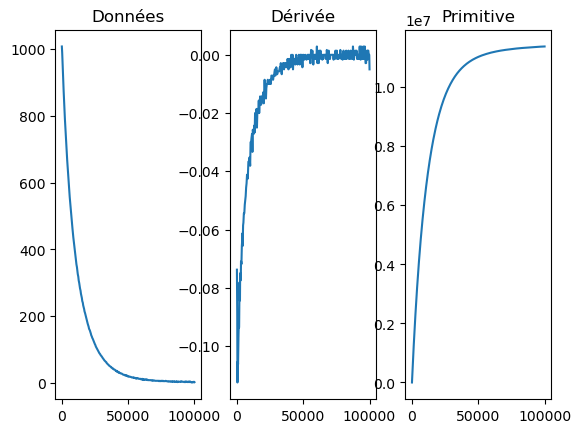
On remarquera que les calculs de dérivées numériques tendent à faire apparaître des “parasites”. Il est conseillé de lisser d’abord la courbe avant de la dérivée.