Signaux sinusoïdaux

Définition

Important

Forme mathématique d’un signal sinusoïdal

Un signal analogique est dit sinusoïdal, si la fonction décrivant la grandeur associée est de la forme :

\[ s(t) = S_m \cos \left ( \omega t +\phi_0 \right ) \]

L’expression mathématique précédente fait apparaître des caractéristiques d’un sinusoïde :

• \(S_m\) est appelée amplitude du signal.

• \(\omega t +\phi\) est appellée phase du signal.

• \(\omega\) est la pulsation du signal, elle est reliée à la période et la fréquence du signal \(T=\frac{2 \pi}{\omega}=\frac{1}{f}\)

• \(\phi\) est appelée phase à l’origine. Il correspond à la phase du signal à \(t=0\) (ou à l’écart de phase, déphasage, (en radians) avec une fonction sinusoïdal qui serait ici maximale en \(t=0\)).

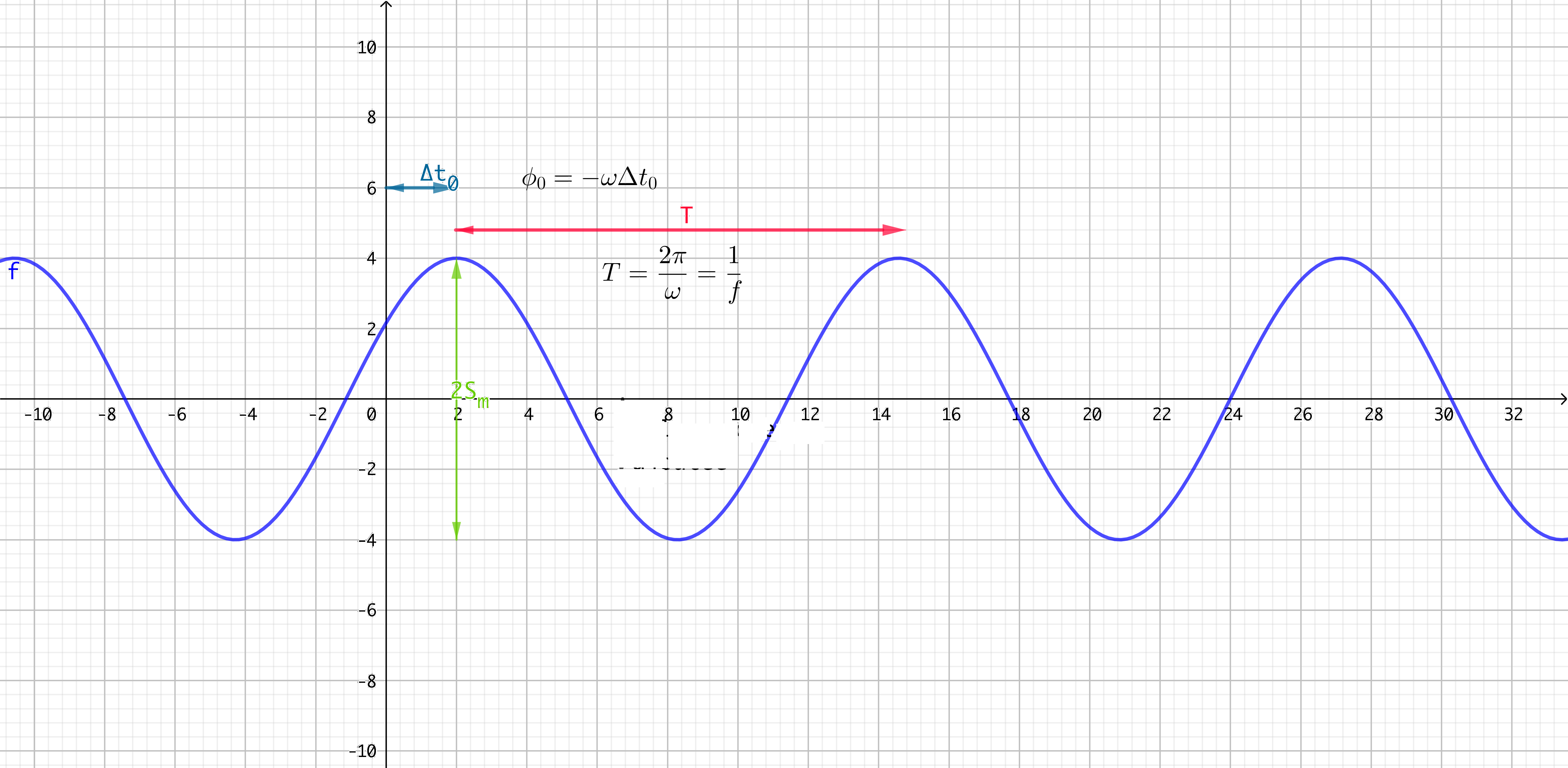
Fig. 1 Sinusoïde

Remarques

• On peut utilise la fonction \(sin\) au lieu de la fonction cosinus. Il faudra néanmoins adapter la notion de phase à l’origine.

• Il arrive qu’on désigne comme signal sinusoïdal un signal de forme \(s(t) = S_m \cos{(\omega t +\phi)} + S_0\) où \(S_0\) est appelé valeur moyenne. Ceci est notamment important en TP. Le terme de valeur moyenne a, comme on le verra ensuite, le même sens que la définition précédente.

• Un signal constant \(S_0\) peut aussi être vu comme un signal sinusoïdal de fréquence… nulle. Cette conception sera fondamental pour la suite.

Attention

L’amplitude n’est PAS l’écart à l’axe des abscisses dans le cas général. Si l’on considère le cas où l’on a ajouté une valeur moyenne, ce n’est pas vrai.

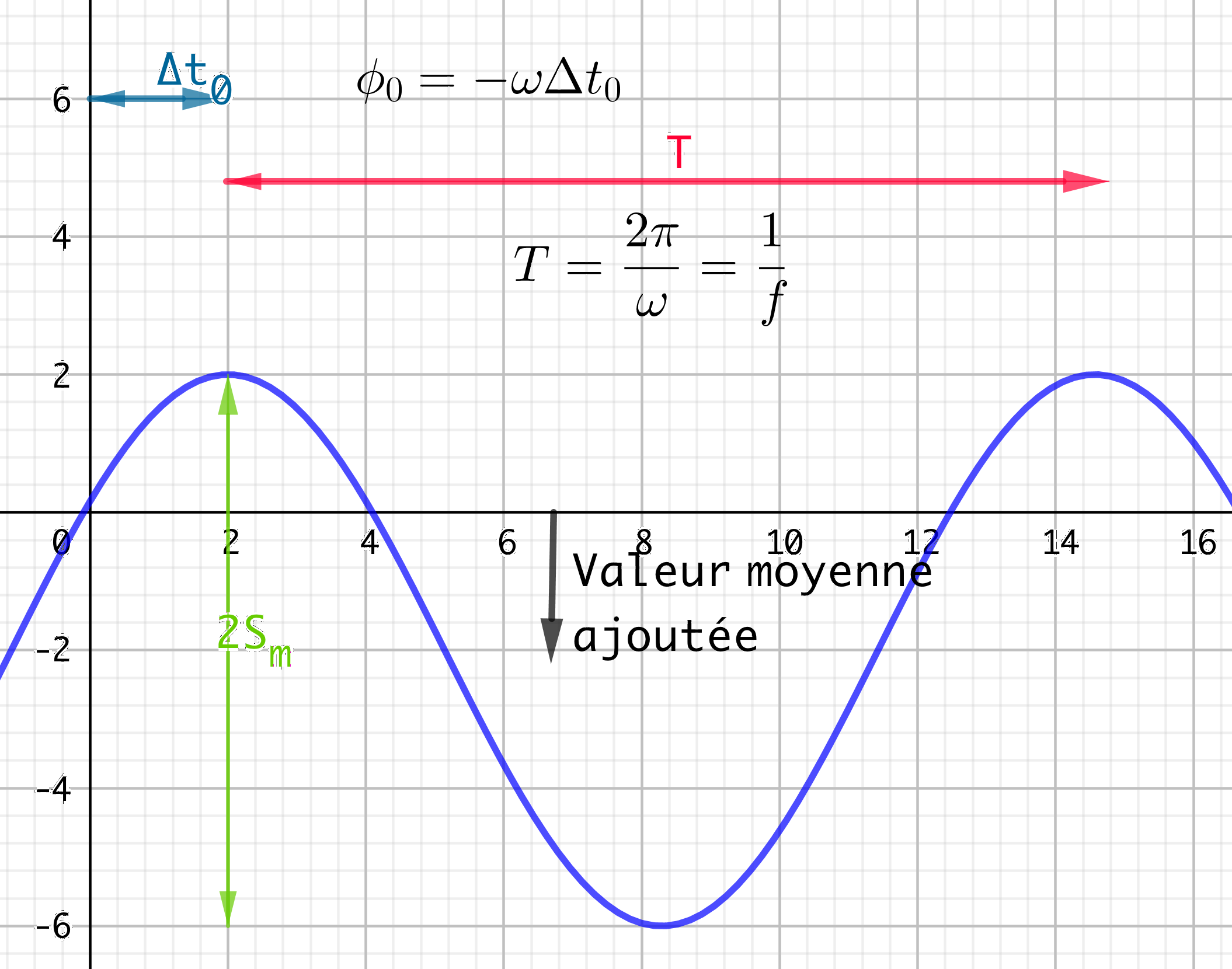
Fig. 2 Sinusoïde avec valeur moyenne

Représentation de Fresnel

Déphasage constant

Fig. 3 Evolution temporelle

Remarquons que lorsque le temps avance, la phase augmente et l’amplitude est constante. La représentation de Fresnel tourne. La vitesse angulaire de rotation dans le plan de Fresnel est la pulsation \(\omega\). D’où l’intérêt de cette grandeur.

Au bout d’une période, la phase a tourner de \(2\pi\) soit une variation de phase \(\Delta \phi = \omega T = 2 \pi\). D’où la relation entre période et pulsation.

Important

Représentation de Fresnel d’un signal sinusoïdal

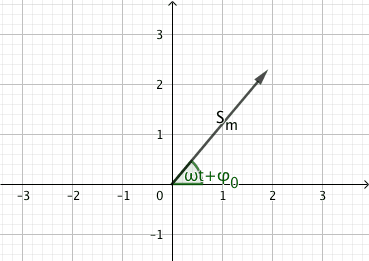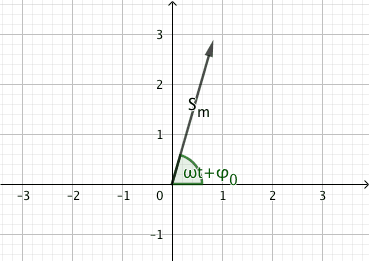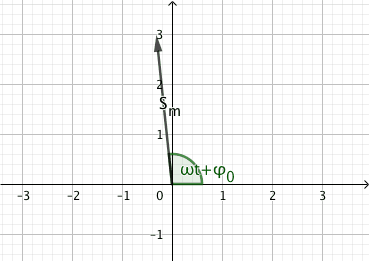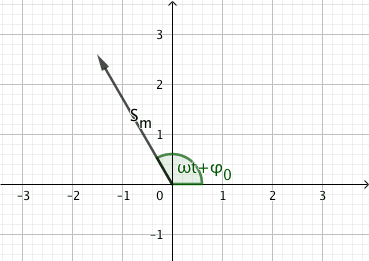
La représentation de Fresnel de la grandeur sinusoïdale s(t) à l’instant t est la représentation dans un plan d’un vecteur \(\overrightarrow{S}\) tel que :

• la norme est l’amplitude de s(t) \(S_m\)

• le vecteur fait avec l’axe des abscisses un angle \(\phi = \omega t + \phi_0\) soit la phase du signal.

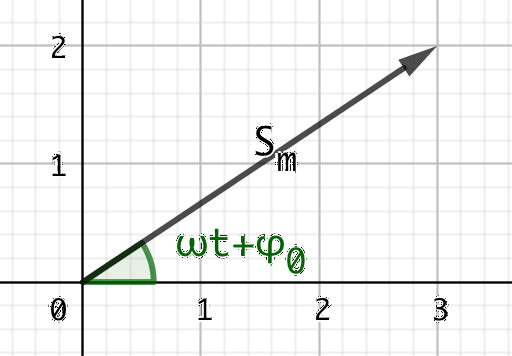
Fig. 4 Représentation de Fresnel

Très souvent, on travaillera avec la représentation de Fresnel à l’instant \(t=0\).

Propriété : Valeurs moyennes et efficaces des sinusoïdes

Important

Fondamental

La valeur moyenne d’un signal sinusoïdal de la forme \(s(t) = S_m \cos{(\omega t + \phi)}\) est nulle.

Si l’on ajoute au signal une valeur constante \(S_0\), alors la valeur moyenne est \(S_0\), d’où le nom de valeur moyenne.

La valeur efficace d’un signal sinusoïdal de la forme \(s(t) = S_m \cos{(\omega t + \phi)}\) est :

\[ \frac{S_m}{\sqrt{2}} \]

Démonstration

• Pour la valeur moyenne :

\[\begin{align*} \left\langle s \right\rangle &= \frac{1}{T} \int_{t=0}^{t=T} S_m \cos{(\omega t + \phi)} dt\\ &= \frac{S_m}{T} \left[ \frac{1}{\omega} \sin{(\omega t + \phi)}\right]_{0}^{T}\\ &= 0 \end{align*}\]

La valeur moyenne d’une constante \(S_0\) est cette constante. Comme la valeur moyenne est un opérateur linéaire, la valeur moyenne de la fonction \(s(t) = S_m \cos{(\omega t + \phi)} + S_0\) est donc bien \(S_0\).

• Pour la valeur efficace :

\[\begin{align*} S_{eff} & = \sqrt{\frac{2}{T} \int_{t=0}^{t=T/2} S_m^2 \cos^2{(\omega t + \phi)} dt}\\ & = \sqrt{\frac{2S_m^2 }{T} \int_{t=0}^{t=T/2} \frac{1}{2} \left ( \cos{2(\omega t + \phi)} + 1 \right) dt }\\ & = \sqrt{\frac{S^2_m}{T} {\left[ \frac{1}{2\omega} \sin{2(\omega t + \phi)}+ t\right]}_{0}^{T/2}}\\ & = \sqrt{\frac{S^2_m}{T} 2T} = \frac{S_m}{\sqrt{2}} \end{align*}\]

Si les deux sinusoïdes sont de même pulsation, la propriété n’est plus vraie, on peut s’en rendre compte en remarquant que le dernier terme (différences des phases) est alors un terme constant dont la valeur moyenne n’est pas forcément nulle.

Important

Valeur efficace d’une somme de deux sinusoïdes

Si l’on somme deux sinusoïdes de fréquences différentes et d’amplitude respectives \(S_{1,eff}\) et \(S_{2,eff}\) alors la valeur efficace de la somme sera :

\[ S_{eff} = \sqrt{S_{1,eff}^2 + S_{2,eff}^2} \]

Démonstration

(2)\[\begin{align} S_{eff} &= \sqrt{\left\langle {(S_1(t) + S_2(t))}^2\right\rangle}\\ &= \sqrt{\left\langle {S_1(t)}^2 + {S_2(t)}^2 + 2 S_1(t) S_2(t)\right\rangle}\\ &= \sqrt{\left\langle{S_1(t)}^2\right\rangle + \left\langle{S_2(t)}^2\right\rangle + \left\langle2 S_1(t) S_2(t)\right\rangle}\\ &= \sqrt{S_{1,eff}^2 + S_{2,eff}^2 + 2 S_1m S_2m \left\langle \cos{(\omega_1 t + \varphi_1)} \cos{(\omega_2 t + \varphi_2)} \right\rangle}\\ &= \sqrt{S_{1,eff}^2 + S_{2,eff}^2 + S_1m S_2m \left\langle \cos{((\omega_1 + \omega_2) t + \varphi_1+\varphi_2)} \right\rangle + S_1m S_2m \left\langle \cos{((\omega_1 - \omega_2) t + \varphi_1 - \varphi_2)} \right\rangle} \\ &= \sqrt{S_{1,eff}^2 + S_{2,eff}^2 + 0 + 0} \end{align}\]

Déphasage en signaux sinusoïdaux

Important

Déphasage

On considère deux signaux sinusoïdaux dont les phases sont \(\varphi_1(t)\) et \(\varphi_2(t)\). Le déphasage \(\Delta \varphi_{2/1}\) du signal 2 sur le signal 1 est défini par

\[ \Delta \varphi_{2/1} = \varphi_2(t) - \varphi_1(t) \]

Si les deux signaux sont de même fréquence/pulsation/période, alors le déphasage entre les deux est constant. Sinon, il varie.

Cas particuliers

• Si le déphasage entre deux signaux est nul, on dit que les signaux sont en phase.

• Si le déphasage entre deux signaux est égal à \(\pi\), on dit que les signaux sont en opposition de phase: le maximum de l’un coïncide avec le minimum de l’autre et réciproquement.

• Si le déphasage entre deux signaux est égal à \(\pm \pi/2\), on dit que les signaux sont en quadrature de phase: le maximum/minimum de l’un coïncide avec le 0 (ou le passage par la valeur moyenne) de l’autre et réciproquement.

Dans le système d’unités S.I., l’unité d’angle est le radian.

Important

Relation entre déphasage et retard temporel Soit deux signaux sinusoïdaux de même pulsation \(\omega\), d’amplitude respectives \(S_1\) et \(S_2\) et de phase à l’origine respectives \(\phi_1\) et \(\phi_2\). Le retard temporel \(\Delta t\) du signal 2 sur le signal 1, représentant l’écart temporel relatif entre deux points des signaux ayant la valeur est relié au déphasage par:

\[ \Delta \phi = - \omega \Delta t \]

Démonstration

On cherche \(\Delta t\) tel que : \(S_1 \cos (\omega t + \phi_1) = S_2 \cos (\omega (t + \Delta t) + \phi_2)\) soit \(\omega t + \phi_1 = \omega (t + \Delta t) + \phi_2\) donc : \(\omega \Delta t = \phi_1 - \phi_2 = - \Delta \phi_{2/1}\)

Intérêt des signaux sinusoïdaux

Les signaux sinusoïdaux sont extrêmement importants en physique. En effet, on les retrouve dans deux cas très répandus:

• Les oscillateurs harmoniques. A l’exemple des systèmes masse-ressort, ces systèmes ont une évolution sinusoïdal. Or nous verrons dans le cours de l’année que les oscillateurs harmoniques se retrouvent partout en physique.

• Tout signal physique peut être vu comme une somme de sinusoïdes d’amplitude, de fréquence et de phase à l’origine bien définie. C’est le principe de la décomposition spectrale qui va être présentée ensuite.