Applications

Contrairement aux exercices du cours qui détaillent les raisonnements pour expliquer les méthodes, seules les réponses finales sont données ici. Il faut s’entraîner à résoudre soi-même tous les exercices proposés ici AVANT DE REGARDER LES RÉPONSES.

Modulation d’amplitude

Exercice

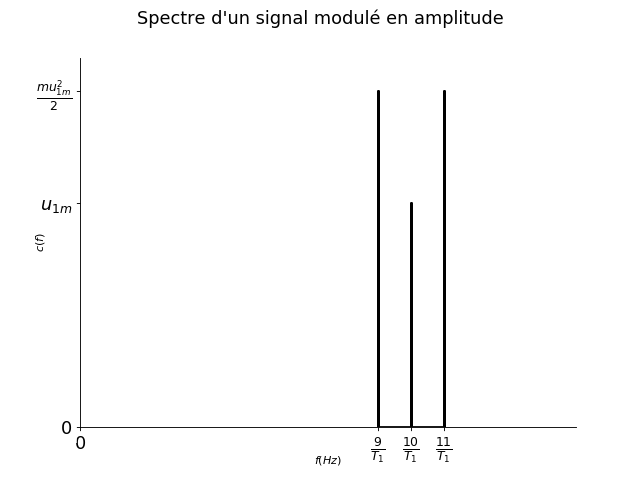
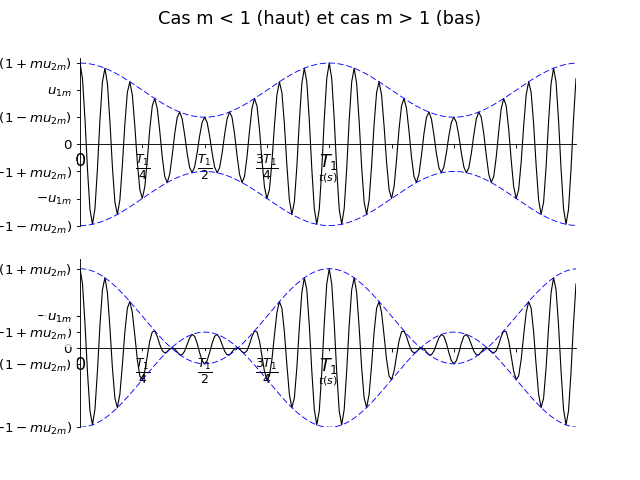
On considère un signal $u_1$ sinusoïdal de période $T_1$ et d’amplitude $u_{1m}$ et un signal $u_2$ sinusoïdal de période $T_2=T_1/10$ et amplitude $u_{2m}=u_{1m}$. On crée à partir de ces deux signaux un troisième signal de la forme : $u_S=u_2\times (1+m{u}_1)$.

1. Donner les expressions temporelles des signaux $u_1$ et $u_2$ en fonction de $T_1,u_{1m}$ et du temps.

2. Justifier que $u_S$ peut être vu comme un signal modulé en amplitude et représenter graphiquement l’allure temporelle de $u_S$.

3. Déterminer le spectre de $u_S$.

Eléments de correction

1.

(3)$$\begin{array}{r}{u}_1(t)=u_{1m}\cos \left(\frac{2\pi }{T_1}t\right)\\ u_2(t)=u_{1m}\cos \left(\frac{20\pi }{T_1}t\right)\end{array}$$

2.

3.

Tracé de spectres

Exercice

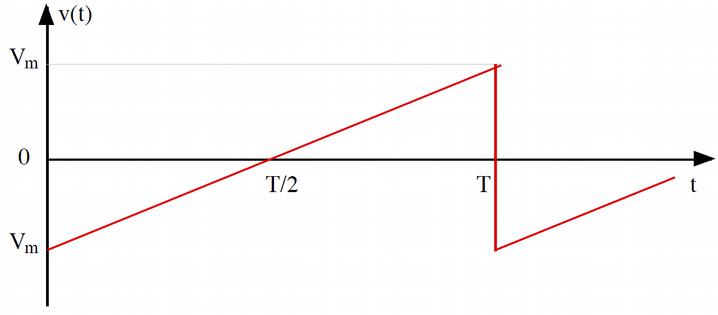
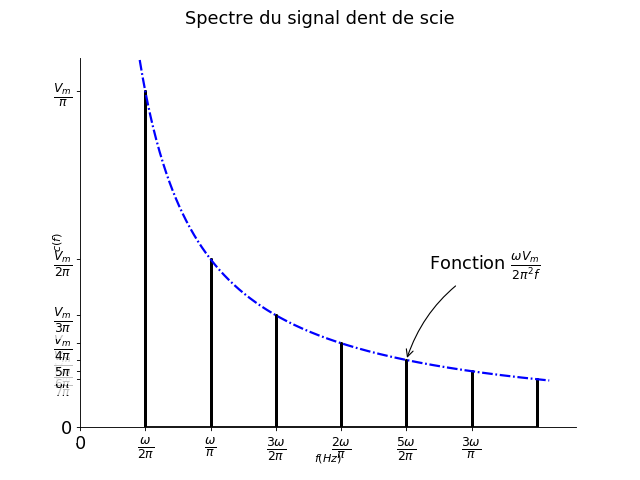
Fig. 16 Signal dent de scie

On considère le signal ``dent de scie’’ dont le tracé temporel est donné ci-contre. On donne aussi sa décomposition en série de Fourier :

$$u(t)=\sum _{n=1}^{+\mathrm{\infty }}\frac{2V_m}{\pi }\frac{(-1{)}^n}{n}\sin n\omega t$$

1. Relier $\omega$ et T. Le justifier.

2. Représenter le spectre de Fourier du signal.

3. Que vaut la valeur moyenne du signal ?

Eléments de correction

1. $T=\frac{2\pi }{\omega }$ attention à bien le justifier.

2.

3. Valeur moyenne nulle.

Exercice

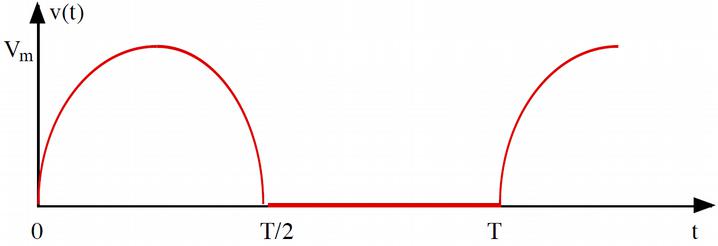
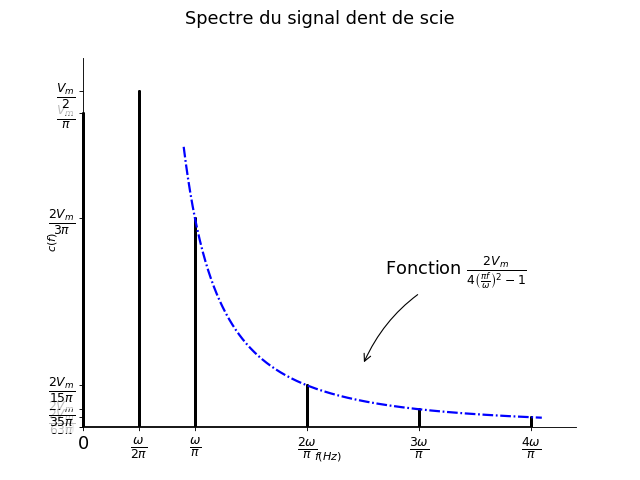
Fig. 17 Signal redressé

On considère le signal ``redressé simple alternance’’ dont le tracé temporel est donné ci-contre. On donne aussi sa décomposition en série de Fourier :

$$u(t)=\frac{V_m}{\pi }+\frac{V_m}{2}\cos \omega t+\sum _{n=1}^{+\mathrm{\infty }}\frac{2V_m}{\pi }\frac{1}{4n^2-1}\sin 2n\omega t$$

1. Relier $\omega$ et T. Le justifier.

2. Représenter le spectre de Fourier du signal.

3. Que vaut la valeur moyenne du signal ?

Eléments de correction

1. $T=\frac{2\pi }{\omega }$ attention à bien le justifier.

2.

3. Valeur moyenne $\frac{V_m}{\pi }$.

Des exercices d’approfondissement qui pour être utiles pour la suite du cours sont disponibles en ligne.