Décomposition spectrale d’un signal physique

Principe de la décomposition spectrale

Important

Principe général

Le principe de la décomposition spectrale est de décomposer un signal \(s(t)\) en une somme de signaux sinusoïdaux de fréquences différentes.

Une fois un signal décomposé en somme de sinusoïde (on parle de composantes spectrales), on obtient plusieurs gammes de fréquences associées à chaque composante spectrale qui vont donner des informations sur le type de signal étudié.

Exemples de décomposition spectrale

• Cas fini On peut décomposer un signal en une somme finie de signaux sinusoïdaux. Le signal \(s(t) = A sin^3 (t)\) peut s’écrire comme la somme :

\[ s(t) = \frac{3A}{4} \sin t - \frac{A}{4} \sin 3t \]

• Cas infini discret

On peut décomposer un signal en une somme infinie discrète de signaux sinusoïdaux. Le signal définie sur \([0 ;T]\) par

\[\begin{split} s(t) = \begin{cases} A \textrm{ si }x \in [0;T/2]\\ -A \textrm{ si }x \in [T/2;T]\end{cases} \end{split}\]

et reproduit à l’infini (signal créneau) peut s’écrire comme la somme :

\[ s(t) = \frac{4 A}{\pi} \sum\limits_{n=0}^{+ \infty} \frac{1}{2n + 1} \sin{[(2n+1) \frac{2 \pi}{T}t]} \]

• Complément - Cas infini continu On peut décomposer un signal en une somme infinie continue de signaux sinusoïdaux, c’est-à-dire que la somme s’effectue sur toutes les valeurs de fréquences appartenant à \(\mathbb{R}\). Une telle somme est plus délicate à écrire avec les connaissances actuelles car cela nécessite l’utilisation d’intégrale et des nombres complexes.

Néanmoins, à titre d’exemple, la fonction \(s(t) = \frac{sin(t)}{t}\) peut se décomposer comme une somme de sinusoïde de toutes les fréquences (réelles) comprises entre \(f = 0\) et \(f = 1/2 Hz\) avec la même amplitude pour chacune. Dans ce cas, on parlera de spectre continu.

Spectre d’une fonction

Important

Spectre d’un signal

Pour une fonction s(t) à spectre discret, on appelle spectre de s, l’ensemble des couples \(\{(f_s,c_S(f))\}\) associant chaque fréquence f des sinusoïdes de la décomposition spectrale à leur amplitude \(c_S(f)\).

On représente le spectre d’une fonction s(t) en représentant chaque coefficient \(c_S(f)\) en fonction de la fréquence correspondante \(f_s\).

L’indice s est marqué ici pour bien montrer que les fréquences et les amplitudes dépendent du signal s considéré.

Cas de la fonction sinus cube

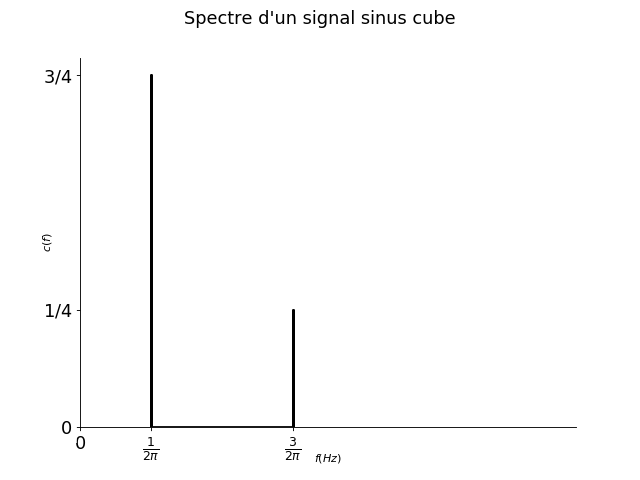
Fig. 5 Spectre du sinus cube

Le spectre de la fonction \(sin^3\) est \(\{(f_1 = \frac{1}{2\pi}, c(f_1) =\frac{3}{4}),(f_2 = \frac{3}{2\pi}, c(f_2) =\frac{1}{4})\}\).

Remarques

• On pourrait écrire plus simplement \(\{(\frac{1}{2\pi}, \frac{3}{4}),( \frac{3}{2\pi}, \frac{1}{4})\}\)

• On tient pas compte du signe (-) car l’amplitude est toujours définie comme positive. Le signe modifie la phase à l’origine (de \(\pi\)) mais celà n’apparaît pas dans le spectre.

Cas de la fonction créneau

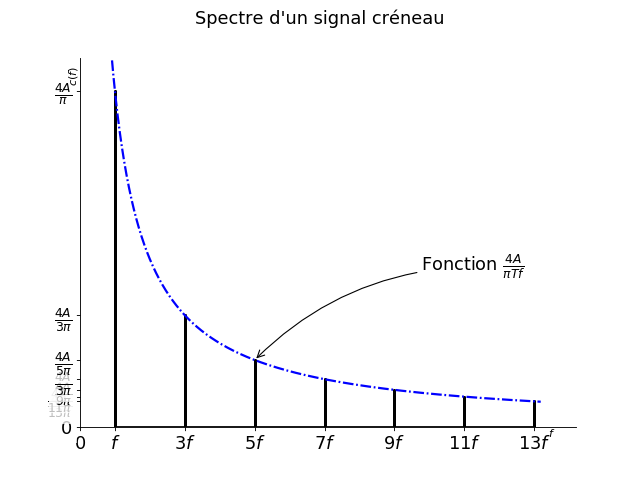
Fig. 6 Spectre d’un créneau

Le spectre de la fonction créneau \(s(t) = \begin{cases} A \textrm{ si }x \in [0;T/2]\\ -A \textrm{ si }x \in [T/2;T]\end{cases}\) fait correspondre aux fréquences \(f_{2n+1} = \frac{2n+1}{T}\) l’amplitude \(\frac{4A}{\pi(2n+1)}=\frac{4A}{\pi T f_{2n+1}}\) avec \(n \in \mathbb{N}\).

On peut tracer le spectre en remarquant qu’il s’agit de tracer la fonction

\[f \longrightarrow \frac{4A}{\pi T f}\]

en fonction de la fréquence \(f\) et de ne prendre que les valeurs entières impaires.

Important

Valeur moyenne

Sur une représentation spectrale, la valeur moyenne se lit à la fréquence 0.

Décomposition des signaux périodiques : Série de Fourier

Il existe des moyens de calculer les \(a_n\) mais la méthode n’est pas à connaître.

Important

Décomposition en série de Fourier

Tout signal périodique s(t) de période T se décompose en une somme infinie (série) de cosinus et de sinus de périodes T/n où n est un entier. On appelle la série correspondante: série de Fourier.

\[ s(t) = a_0 + \sum\limits_{n=1}^{+ \infty} (a_s(n) \cos(\frac{2 \pi n}{T}t)+b_s(n) \sin(\frac{2 \pi n}{T}t)) \]

Ou, comme on l’écrira souvent pour pouvoir représenter le spectre :

\[ s(t) = a_0 + \sum\limits_{n=1}^{+ \infty} (c_s(n) \cos(\frac{2 \pi n}{T}t + \phi_s(n))) \]

\[ s(t) = a_0 + \sum\limits_{n=1}^{+ \infty} (c_s(n) \sin(\frac{2 \pi n}{T}t + \psi_s(n))) \]

Les coefficients \(c_s(n)\) sont les amplitudes des composantes spectrales comme étudiées précédemment. On les définit ici directement en fonction de n qui correspond au rang de la n-ième composante spectrale et on les appelle des coefficients de Fourier.

Dans le cas d’un signal périodique, ces composantes sont appelées des harmoniques. La composante spectrale de même période que le signal (elle existe forcément) est appelée fondamental.

On reconnaîtra que \(a_0\) correspond à la valeur moyenne du signal.

Exemple : Spectre du signal triangle

Outre le cas du signal créneau, on peut aussi citer le cas du signal triangle \(s(t) = \begin{cases} a (t - \frac{T}{4}) \textrm{ si }x \in [0;T/2]\\ -a (t - \frac{3T}{4}) \textrm{ si }x \in [T/2;T]\end{cases}\) dont les coefficients de Fourier sont \(c_s(n) = \frac{8aT}{\pi^2 n^2}\) lorsque n est impaire et 0 sinon.

On remarquera et c’est important de le retenir que les harmoniques du signal créneau ont une amplitude qui décroît en \(1/n\) et les harmoniques du triangle ont une amplitude qui décroît en \(1/n^2\) : on tend donc plus vite vers la forme triangle que vers la forme créneau.

Simulation

Vous pourrez trouver ici une simulation réalisée en Geogebra permettant de construction une fonction périodique par sommation de ses composantes de Fourier.