Méthodes : Calculs divers
Contents
Méthodes : Calculs divers#
Les corrections sont en ligne.
Valeur efficace et valeur moyenne#
Exercice (correction en ligne)
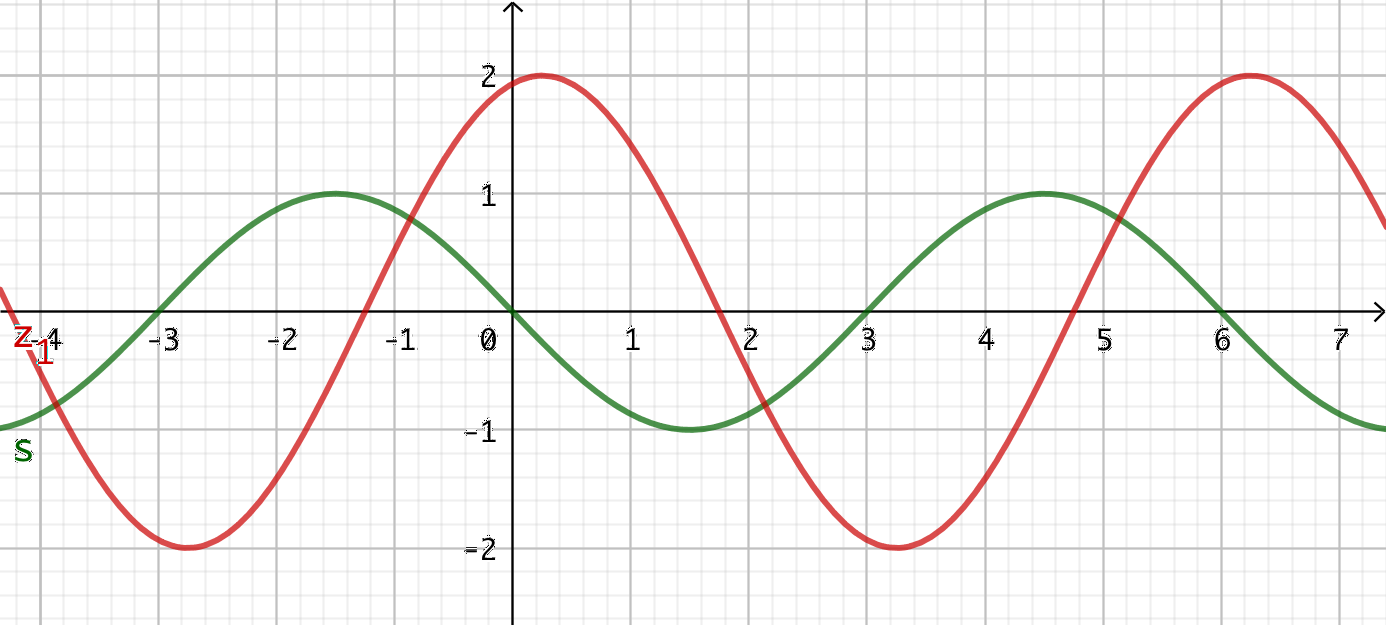
Calculer la valeur moyenne puis efficace du signal “créneau” de période T, s(t) défini par:
Correction
Valeur moyenne : On utilise la définition de la valeur moyenne et l’on sépare l’intégrale en deux parties :
\[ \left\langle s \right\rangle = \frac{1}{T} \left (\int_{t=0}^{t=T/2} A dt + \int_{t=T/2}^{t=T} - A dt \right ) = \frac{1}{T}(\frac{AT}{2} - \frac{AT}{2}) = 0 \]Valeur efficace : On utilise la définition de la valeur efficace et l’on sépare l’intégrale en deux parties :
\[ S_{eff} = \sqrt{\int_{t=0}^{t=T/2} A^2 dt + \int_{t=T/2}^{t=T} {(- A)}^2 dt} = \sqrt{\frac{1}{T}(\frac{A^2T}{2} + \frac{A^2T}{2})} = A \]
Exercice (correction en ligne)
Calculer la valeur moyenne puis efficace du signal “triangle” de période T, s(t) défini par:
Correction
Valeur moyenne : On utilise la définition de la valeur moyenne et l’on sépare l’intégrale en deux parties :
\[ \left\langle s \right\rangle = \frac{1}{T}\left (\int_{t=0}^{t=T/2} a (t-T/4) dt + \int_{t=T/2}^{t=T} - a (t - 3T/4) dt \right ) = \frac{a}{T}(0 + 0) = 0 \]Valeur efficace : On utilise la définition de la valeur efficace et l’on sépare l’intégrale en deux parties :
\[ S_{eff} = \sqrt{\int_{t=0}^{t=T/2} a^2 {(t - T/4)}^2 dt + \int_{t=T/2}^{t=T} a^2 {(t - 3T/4)}^2 dt} = \sqrt{\frac{a^2}{T}(\frac{T^3}{96} + \frac{T^3}{96})} = \frac{aT}{4 \sqrt{3}} \]
Danger
On remarquera que \(S_{eff} \ne \sqrt{\left\langle s \right\rangle^2}\)
Etudier les caractéristiques d’un sinusoïde#
L’objectif est
d’apprendre à écrire correctement l’expression mathématique d’un sinusoïde connaissant ou en mesurant ses caractéristiques.
de faire l’inverse : obtenir les caractéristiques d’un sinusoïde et tracer son graphique à partir de son expression mathématique.
Exercice
Donner l’expression mathématique s(t):
d’un sinusoïde de pulsation \(4\omega\), d’amplitude 2a et de phase à l’origine \(-\pi/5\).
d’un sinusoïde de période \(2T/3\), d’amplitude 4a (si rien n’est précisé, on considère que la phase à l’origine est nulle).
d’un sinusoïde de fréquence 3f, d’amplitude 2a, de valeur moyenne - \(S_1\) et de phase à l’origine \(\pi/3\).
Correction
\(s(t) = 2a \cos {(4 \omega t - \frac{\pi}{5})}\)
La pulsation vaut alors \(\omega = \frac{6\pi}{2T}\) donc \(s(t) = 4a \cos {(\frac{3\pi}{T} t )}\)
La pulsation vaut alors \(\omega = 2\pi \times 3f\) donc \(s(t) = 2a \cos {(6\pi f t + \frac{\pi}{3})} - S_1\)
Attention
Il faut faire attention à bien différencier le sens physique d’une grandeur et les notations utilisées. Ainsi, même si dans cet exercice on utilise les notations T et f, elles ne correspondent pas aux périodes et fréquences des signaux. Le sens physique s’obtient par analyse des équations mathématiques, pas par analyse du nom de la grandeur.
Exercice
Réaliser la représentation graphique de s(t) pour les expressions précédentes. On prendra a=1, T=1, \(\omega = \pi\), f=1, \(S_1=2\)
Correction
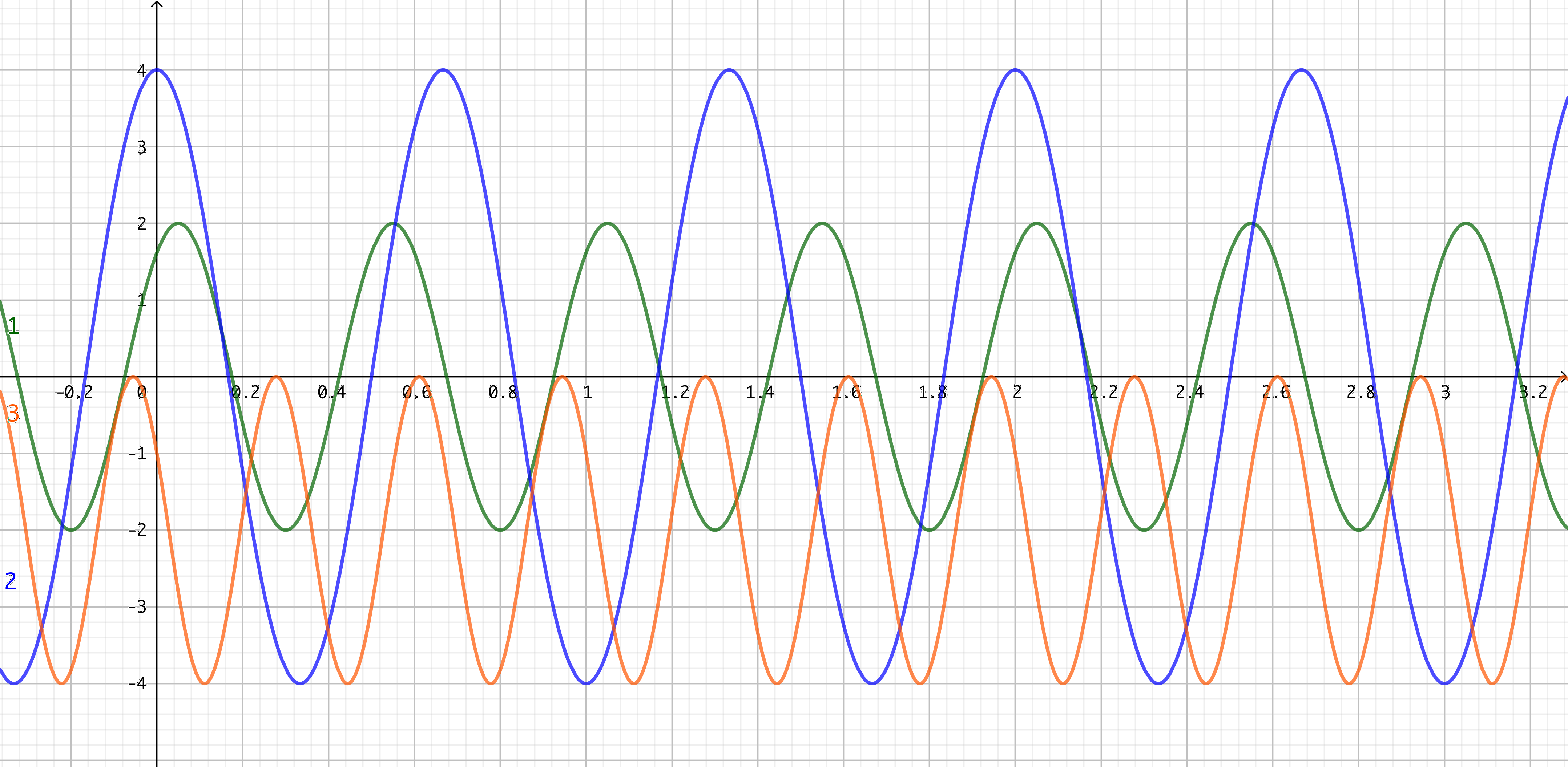
Important
Lien retard temporel et phase
La valeur moyenne déterminer l’axe de symétrie du sinusoïde et l’amplitude l’écart à cet axe de symétrie (les valeurs extrêmes).
On a utilisé la relation \(\phi_0 = - \omega t_1\) pour calculer le retard temporel où \(t_1\) est le temps où la fonction cosinus sera maximale (puisque la phase est alors nulle).
On a ensuite représenté des points particuliers pour faciliter le tracé (points extrêmes, passage par la valeur moyenne) en utilisant la valeur de la période de chaque signal à partir de \(t_1\).
Exercice
Donner les caractéristiques (période, fréquence, pulsation, amplitude, valeur moyenne, phase à l’origine) des signaux suivants :
\(s(t) = \frac{1}{2k + 1} \sin{(2k+1) \omega t}\)
\(s(t) = 7\omega \cos(2f t + 3)\)
\(s(t) = 3a \cos(\frac{2\pi n}{T}t) + 4c\)
Correction
La lecture des caractéristiques ne se fait pas par rapport au nom des grandeurs mais à leur position dans la structure mathématique. Ainsi :
L’amplitude est le facteur multiplicatif du sinusoïde \(\boxed{A}\sin \omega t + \phi\).
La pulsation est le facteur multiplicatif devant le temps \(A\sin \boxed{\omega} t + \phi\).
\(s(t) = \boxed{\frac{1}{2k + 1}} \sin{\boxed{(2k+1) \omega} t} \) donc
Amplitude : \(\frac{1}{2k + 1}\)
Pulsation\((2k + 1) \omega\)
Période : \(\frac{2\pi}{(2k+1)\omega}\)
Fréquence : \(\frac{(2k+1) \omega}{2 \pi}\)
Valeur moyenne nulle
Phase à l’origine nulle
\(s(t) = \boxed{7\omega} \cos(\boxed{2f} t + 3)\)
Amplitude : \(7 \omega\)
Pulsation\(2f\)
Période : \(\frac{2\pi}{2f}\)
Fréquence : \(\frac{f}{\pi}\)
Valeur moyenne nulle
Phase à l’origine : 3
\(s(t) = \boxed{3a} \cos(\boxed{\frac{2\pi n}{T}}t) + 4c\)
Amplitude : \(3a\)
Pulsation\(\frac{2 \pi n}{T}\)
Période : \(T/n\)
Fréquence : \(\frac{n}{T}\)
Valeur moyenne 4c
Phase à l’origine : nulle
Calculer un déphasage#
Le but de cet exercice est de comprendre la notion de déphasage et les méthodes d’études associées.
Attention
Attention, on ne peut mesurer directement un déphasage (en radian) sur un graphique temporel. On mesure un retard temporel.
Correction
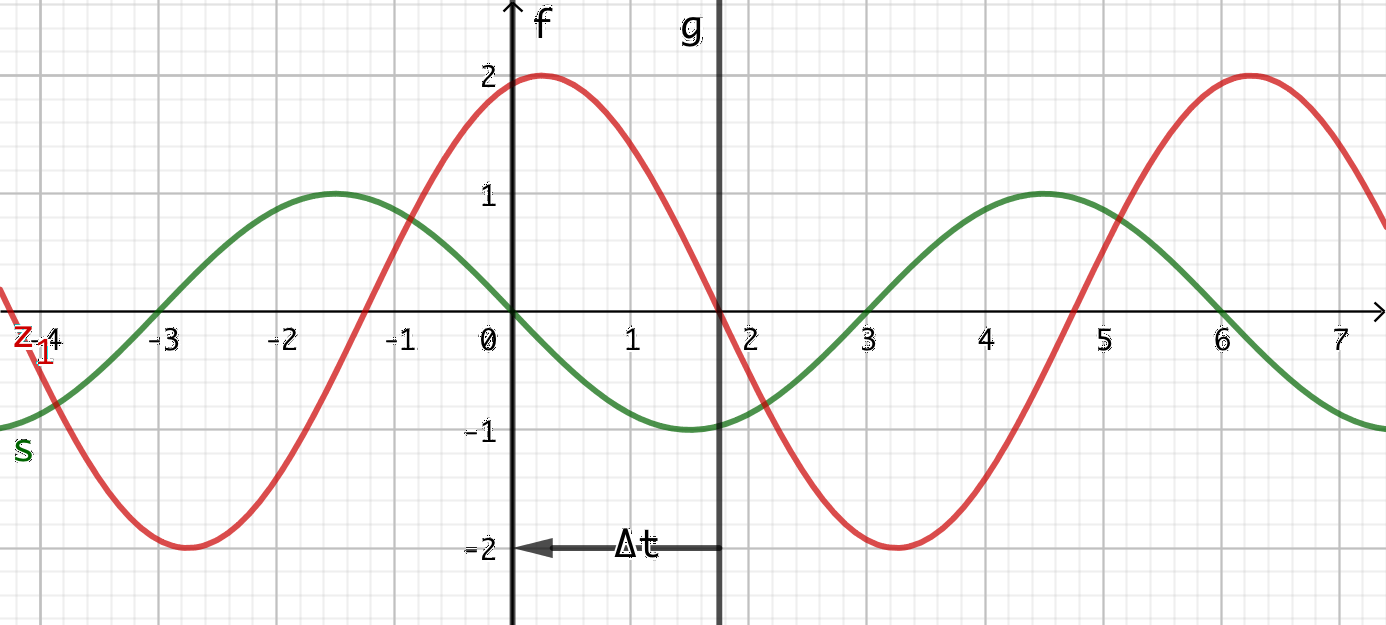
Commençons par mesurer le retard temporel du signal vert sur le signal rouge. C’est une grandeur algébrique, il faut donc tenir compte de l’ordre des deux signaux. Ici, le signal vert est en avance, donc le retard est négatif.
Ce retard se mesure entre deux points ayant la même valeur en ordonnée. Il est conseillé de mesurer le retard entre deux points où la fonction s’annule (ou atteint sa valeur moyenne) pour des questions de précision. On mesure ici \(\Delta t = - 1.8 s\).
On doit ensuite utiliser la relation prouvée précédemment \(\Delta \phi = - \omega \Delta t\). La pulsation s’obtient en mesurant la période. Ici T = 6s donc \(\omega = \pi / 3= 1 \rm{rad.s^{-1}}\).
Il vient \(\Delta \phi = 1.8 \rm{rad}\)
Tracer le spectre d’un signal périodique#
Exercice
On reprend le signal triangle :
dont la décomposition en série de Fourier est :
Justifier que ce signal est périodique de période T.
Représenter le spectre du signal.
Correction
Période du signal : Dans une décomposition en série de Fourier, la période du signal correspond à la période du fondamental, donc de la composante de plus basse fréquence. Ici, c’est pour n=0, soit une pulsation (on ne peut lire directement qu’une pulsation) \(\frac{2\pi}{T}\) donc une période T
Tracé du spectre : La méthode pour tracé un spectre connaissant la décomposition spectrale est :
Déterminer les pulsations puis les fréquences qui composent le spectre. On a ici une série. La pulsation de chaque terme se lit dans le sinus \(\sin[\boxed{(2 n +1) \frac{2\pi}{T}} t]\). Les pulsations du signal sont donc les pulsations \((2 n +1) \frac{2\pi}{T}\) donc les fréquences \(f_n = \frac{2n+1}{T}\). On peut alors placer les fréquences sur un graphique.
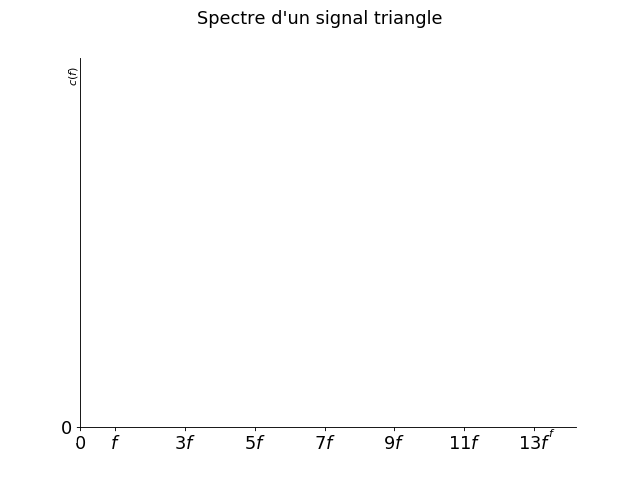
Fig. 12 Fréquences du signal#
Déterminer les amplitudes associées à des fréquences. Si les fréquences sont isolées, on lit l’amplitude comme le facteur devant le sinus/cosinus. Dans le cas d’une somme, on va déterminer la fonction qui associe le n-ième rang (puis la fréquence) à l’amplitude. Ici l’amplitude de chaque sinusoïde a pour expression \(c(n) = \frac{8aT}{\pi^2(2n+1)^2}\). L’étude précédente (\(2n+1 = f_n T\)) permet d’exprimer \(c_n\) en fonction de \(f_n\):
\(c(f_n) = \frac{8aT}{\pi^2 T^2 f_n^2}\)
On trace alors la fonction \(c(f)\) et on trace des traits représentant les amplitudes pour les composantes spectrales réellement présentes.
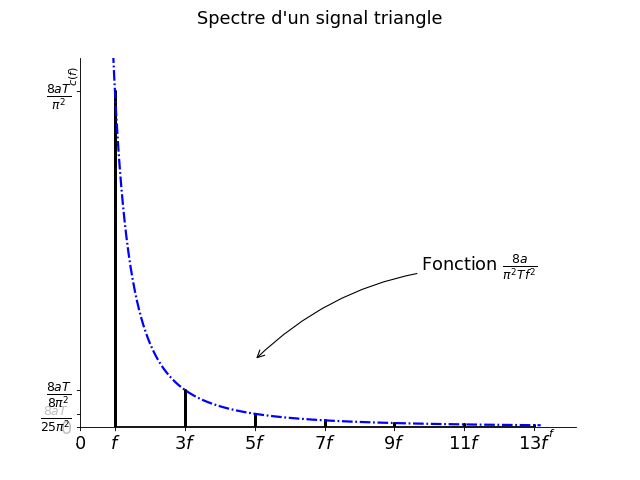
Fig. 13 Fréquences du signal#