Activité : Etudier une modulation en amplitude.

La correction est en ligne et une simulation permet de jouer sur les paramètres d’une modulation est disponible ici.

Nous allons étudier le principe de décomposition sur un cas simple où un signal se décompose en une somme finie de composantes spectrales.

La méthode de linéarisation des produits de sinusoïdes, basées sur les relations usuelles en trigonométrie est à maîtriser impérativement. La méthode de tracé du signal est aussi très important.

Exercice

On considère deux signaux sinusoïdaux \(u_1(t)\) et \(u_2(t)\) de fréquence \(f_1\) et \(f_2\) d’amplitude \(u_{1m}\) et \(u_{2m}\) de phase à l’origine nulle tous les deux. On multiplie les deux signaux \(u_S(t) = k u_1(t) \times u_2(t)\) avec k une constante connue.

• Donner les expressions de \(u_1(t)\) et \(u_2(t)\) puis de \(u_S(t)\)

• On prend \(f_1 = 10 f_2\) et \(u_{2m} = 2 u_{1m}\), représenter graphiquement \(u_S\). Justifier le terme de modulation en amplitude. Où ce principe est utilisé?

• Montrer que le signal se décompose comme la somme de deux composantes spectrales dont on déterminera la fréquence et l’amplitude.

• Représenter le spectre du signal \(u_S\).

Correction

1. Les deux signaux entrant s’écrivent : \(u_1(t) = u_{1m} \cos (2 \pi f_1 t)\) et \(u_2(t) = u_{2m} \cos (2 \pi f_2 t)\)

Il vient pour le signal de sortie : \(u_S(t) = k u_{1m} u_{2m} \cos (2 \pi f_1 t) \cos (2 \pi f_2 t) \)

2.

Le tracé d’une telle fonction ne doit pas nécessiter une calculatrice et doit faire apparaître des caractéristiques précises :

• On commence par tracer l’enveloppe (trait discontinu) qui correspond à l’amplitude variable \(k u_{1m} u_{2m} \cos (2 \pi f_2 t)\) et son opposé (la fonction \(u_S(t)\) atteindra ces enveloppes quand \(\cos (2 \pi f_1 t)\) sera égale à 1 et -1. Cela dessine les valeurs maximales accessibles, d’où le nom d’enveloppe. Il faut repérer les valeurs maximales et minimales de l’enveloppe, ici \(k u_{1m} u_{2m}\) et \(-k u_{1m} u_{2m}\)

• On trace alors la fonction comme un sinusoïde contenu dans l’enveloppe. Il faut faire attention au nombre de sinusoïde dans une période (il doit ici y en avoir 10 car \(f_1 = 10 f_2\))

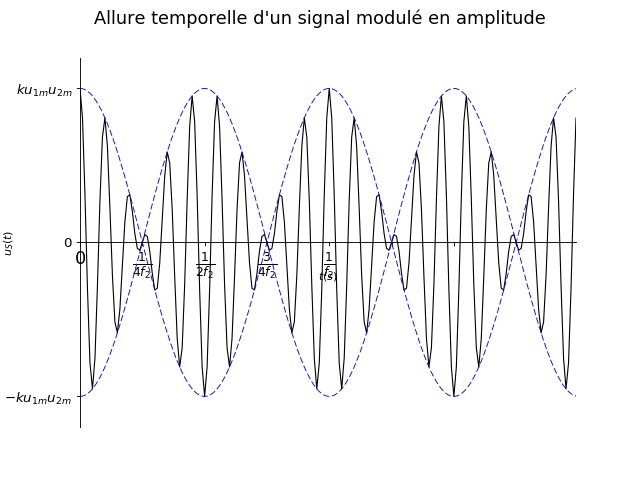
Fig. 14 Modulation d’amplitude

3. Pour obtenir le spectre lorsque le signal est un produit de sinusoïde, il faut procéder par linéarisation.

\[ u_S(t) = \frac{k u_{1m} u_{2m} }{2} \left( \cos(2 \pi (f_1 + f_2) t) + \cos(2\pi (f_1 - f_2)t) \right) \]

Le spectre est donc composée de deux composantes de fréquences \(f_1 + f_2 = 11 f_2\) et \(f_1 - f_2 = 9 f_2\). Elles ont toutes les deux une amplitude \( \frac{k u_{1m} u_{2m} }{2} \).

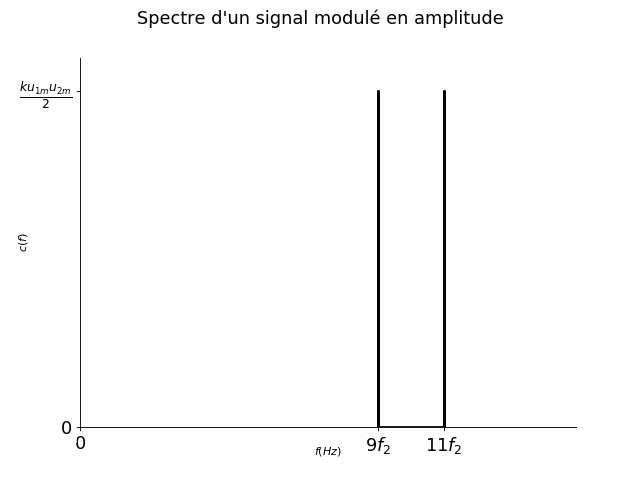
Fig. 15 Spectre du signal modulé

Important

A retenir

Il faut savoir :

• reconnaître un cas de modulation d’amplitude : un produit de sinusoïdes dont la fréquence de l’un est grande devant la fréquence de l’autre.

  • On peut écrire \(u_S(t)\) sous la forme : \( \left [ k u_{1m} u_{2m} \cos (2 \pi f_2 t) \right ] \cos (2 \pi f_1 t)\). Puisque \(f_2\) est faible, on peut considérer que sur une période du signal rapide de fréquence \(f_1\), la grandeur \(k u_{1m} u_{2m} \cos (2 \pi f_2 t)\) est quasi-constante et représente donc sur une période, l’amplitude du sinusoïde \( \cos (2 \pi f_1 t)\). Mais comme d’une période à l’autre l’amplitude varie, on parle de modulation d’amplitude.

• Le signal lent de fréquence \(f_2\) est appelé signal modulant et le signal rapide est appelé signal porteur. Le signal sortant est appelé signal modulé.

• réaliser un tracé correct d’un signal modulé en amplitude en tenant du rapport de fréquences

• Linéariser le produit pour obtenir le spectre du signal.