7. La bibliothèque numpy.random#

La sous-bibliothèque numpy.random sera très utile en physique et en chimie pour les calculs d’incertitude (simulation de Monte-Carlo). Elle propose des fonctions qui permettent de simuler un tirage aléatoire suivant une loi choisi. On présente deux fonctions en particulier : uniform et normal.

7.1. Rappel : Importation de la bibliothèque#

import numpy.random as rd  # Il est conseillé d'importer les bibliothèques au début de votre script

"""On importe aussi les autres bibliothèques scientifiques qui vont être utiles"""
import matplotlib.pyplot as plt
import numpy as np

7.2. Signature des fonctions usuelles#

On ne présente pas ici les loi de probabilités. Voici quelques informations :

La syntaxe :

  • rd.uniform(a, b, N) va réaliser N tirages aléatoires suivant une loi uniforme entre les valeurs a et b.

  • rd.normal(m, s, N) va réaliser N tirages aléatoires suivant une loi normale d’espérance m et d’écart-type s

Note

Les deux fonctions renvoient un vecteur numpy

%time  # Permet d'afficher le temps d'exécution (pas à connaître). 
# On verra qu'on peut ainsi faire un grande nombre de simulation rapidement

N = 1000000  # Nombre d'échantillons
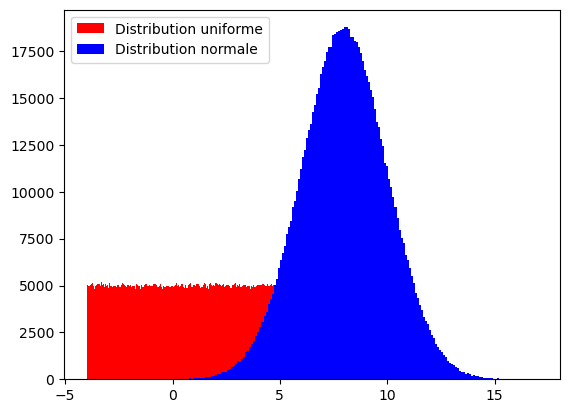
X1 = rd.uniform(-4, 6, N)  # Distribution uniforme entre -4 et 6
X2 = rd.normal(8, 2, N)  # Distribution normale de moyenne 8 et d'écart-type 2

f, ax = plt.subplots()
ax.hist(X1, bins='rice', color='red', label='Distribution uniforme')
ax.hist(X2, bins='rice', color='blue', label='Distribution normale')
ax.legend()
plt.show()

CPU times: total: 0 ns
Wall time: 0 ns
../_images/num_random_3_1.png

7.3. Intérêt de la vectorialisation#

Les fonctions uniform et normal renvoient des vecteurs numpy. On peut donc réaliser des opérations termes à termes entre deux vecteurs issus de ces fonctions.

Exemple

On dispose de deux variables aléatoires \(X_1\) et \(X_2\) qui suivent deux lois :

  • \(X_1\) suit une loi uniforme entre 2 et 4

  • \(X_2\) suit une loi normale d’espérance 1 et d’écart-type 1.

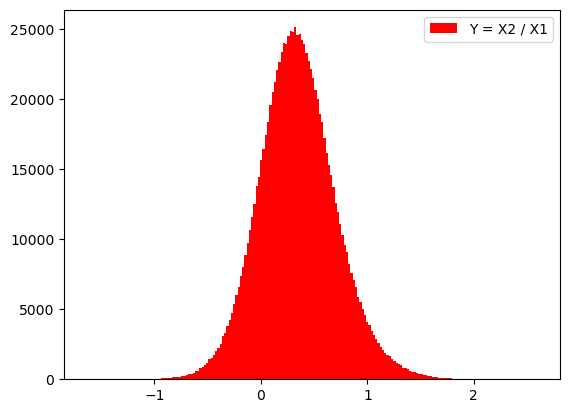
On désire connaître la loi que suit la variable définie par \(Y = X_2 / X_1\). Pour le savoir, on va réaliser N tirages de \(X_1\) et \(X_2\) et évaluer leur rapport à chaque fois. On obtient ainsi N échantillons simulés de \(Y\) dont on va tracer l’histogramme.

N = 1000000
X1 = rd.uniform(2, 4, N)  # N simulations de X1
X2 = rd.normal(1, 1, N)  # N simulations de X2
Y = X2 / X1  # On utilise la vectorialisation des opérations pour estimer Y

f, ax = plt.subplots()
ax.hist(Y, bins='rice', color='red', label='Y = X2 / X1')
ax.legend()
plt.show()
../_images/num_random_5_0.png

Note

Ce principe consistant à simuler ungrand nombre de tirages des \(X_i\) pour obtenir la distribution de \(Y\) puis sa valeur moyenne et son écart-type s’appelle simulation de Monte-Carlo. Elle sera utilisée en physique et en chimie pour estimer des incertitudes de mesure.

7.4. Caractéristique d’une distribution#

numpy permet aussi de remonter à des grandeurs utiles sur une distribution statistique : sa moyenne et son écart-type. Ces fonctions seront aussi utiles avec des données expérimentales.

  • mean(vec) renvoie la moyenne des éléments du vecteur numpy vec

  • std(vec, ddof=1) renvoie l’écart-type des éléments du vecteur numpy vec

On ne rentre pas les détails, mais l’option ddof=1 est importante sinon le calcul de std ne sera pas correct.