5. Régression linéaire#

Il arrive fréquemment qu’on veuille ajuster un modèle théorique sur des points de données expérimentaux. Le plus courramment utilisé pour nous est l’ajustement d’un modèle affine \(Y = aX + b\) à des points expérimentaux \((x_i, y_i)\) (i allant de 1 à k). On veut connaître les valeurs de \(a\) et \(b\) qui donne une droite passant au plus près des points expérimentaux (on parle de régression linéaire).

5.1. Modélisation du problème#

Nous allons donner, sans rentrer dans les détails un sens au terme “au plus près”. La méthode proposée ici s’appelle la méthode des moindres carrés. Dans toute la suite la méthode proposée suppose qu’il n’y a pas d’incertitudes sur les abscisses \(x_i\) ou qu’elles sont négligeables devant celles sur les \(y_i\).

Cf. les cours de physique et chimie pour la notion d’incertitude de mesure. On gardera l’idée qu’elle quantifie la variabilité de la mesure d’une grandeur.

Du fait des incertitudes (de la variabilité des mesures), les points \((x_i, y_i)\) ne sont jamais complètement alignés. Pour une droite d’ajustement \(y_{adj} = ax + b\), il y aura un écart entre \(y_i\) et \(y_{adj}(x_i)\). La méthode des moindres carrés consiste à minimiser globalement ces écarts, c’est-à-dire à minimiser par rapport à a et b la somme des carrés des écarts, soit la fonction :

\[ \Gamma(a, b) = \sum_{i=1}^{i=k} \left( y_i - y_{adj}(x_i) \right)^2 = \sum_{i=1}^{i=k} \left( y_i - (a x_i + b) \right)^2 \]

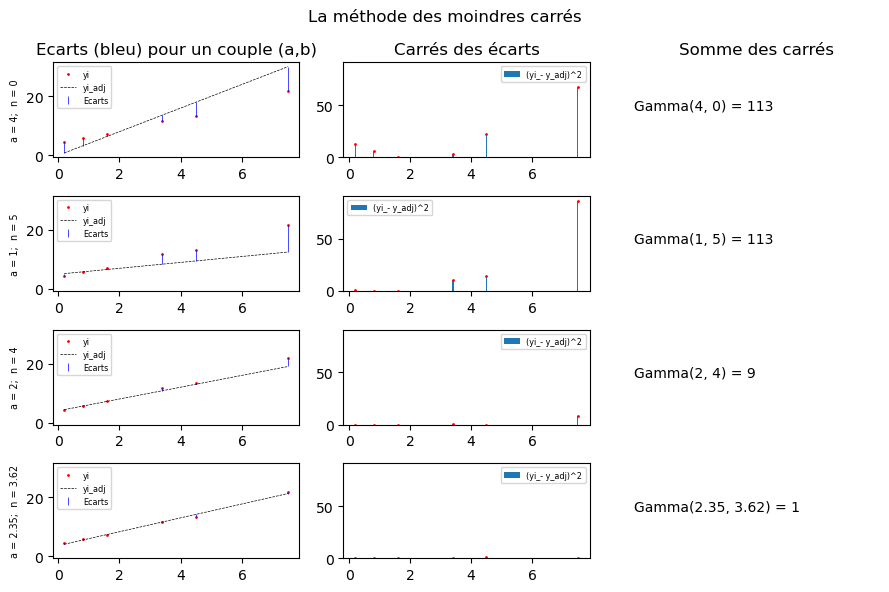
Les tracés ci-après montre le passage (gauche à droite) des écarts modèle-mesures pour un couple \((a,b)\) au calcul de \(\Gamma\) pour quelques couples de valeurs \((a,b)\). On remarque que plus \(\Gamma(a, b)\) est faible, plus la droite d’ajustement semble passer près des points de mesure.

../_images/np_polyfit_1_0.png

On ne présente pas ici les calculs permettant de minimiser une fonction de plusieurs variables mais on admettra que dans le cas précédent, les valeurs \(\hat a\) et \(\hat b\) qui minimise \(\Gamma(a,b)\) sont calculables analytiquement. Elles ont pour expression (pas à connaître par coeur) :

\[\begin{split} \begin{cases} \hat a &= \frac{\frac{1}{k}\sum_i x_i y_i - \left (\frac{1}{k}\sum x_i\right ) \left (\frac{1}{k}\sum y_i\right )}{\frac{1}{k}\sum_i x_i^2 - {\left (\frac{1}{k}\sum x_i\right )}^2}\\ \hat b &= \overline{y} - \hat a \overline{x} \end{cases} \end{split}\]

avec \(\overline{y}\) la moyenne des \(y_i\) et \(\overline{x}\) la moyenne des \(x_i\).

5.2. numpy.polyfit#

5.2.1. Syntaxe#

La majorité des méthodes numériques proposées par les logiciels utilisent la méthode des moindres carrés (DROITEREG sous Excel et Libreoffice par exemple). C’est aussi le cas de la fonction polyfit de la bibliothèque numpy. Sa syntaxe (version simple) est:

polyfit(x, y, deg)

où :

  • x est le vecteur contenant les valeurs des abscisses

  • y est le vecteur contenant les valeurs des ordonnées

  • deg le degré (un entier) du polynôme d’ajustement. Pour nous, ce sera toujours 1.

polyfit permet en effet un ajustement polynomial par un polynôme de degré supérieur à 1.

Cette fonction renvoie un vecteur contenant les coefficient du polynôme par degré décroissants. Ainsi, pour un degré 1 et si on écrit la droite d’ajustement \(Y = aX + b\), le vecteur aura la forme : array([a, b])

5.2.2. Méthode d’utilisation.#

Réaliser une régression linéaire demande de la rigueur, il ne faut pas simplement appliquer la formule précédente. Vous devez :

  1. Tracer le nuage de points des \((x_i, y_i)\) et vérifier qu’ils sont globalement alignés. Il ne sert à rien de faire une régression linéaire s’il y a des points qui dévient clairement d’un modèle affine ou si la tendance n’est pas affine.

  2. Ensuite seulement, utiliser la fonction polyfit pour obtenir les paramètres d’ajustement optimaux.

  3. Représenter la droite d’ajustement sur le même graphique pour vérifier qu’elle est cohérente avec les points de mesures. Des méthodes de tests seront présentées plus précisément en physique et en chimie.

On ne trace pas des ajustments affine à tout va. Il est notamment inutile de tracer une droite d’ajustement si le modèle théorique attendue n’est pas affine…

5.2.3. Un exemple de syntaxe#

import numpy as np
import matplotlib.pyplot as plt

""" Fausses (!) données expérimentales """
xi = np.array([0.2, 0.8, 1.6, 3.4, 4.5, 7.5])
yi = np.array([4.4, 5.7, 7.2, 11.7, 13.3, 21.8])

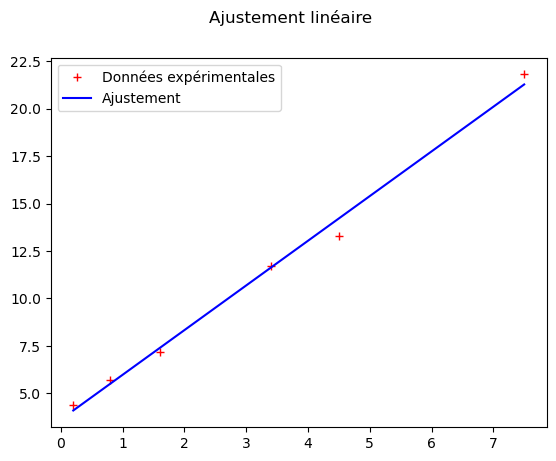
"""Tracé graphique pour test visuel"""
f, ax = plt.subplots()
f.suptitle("Ajustement linéaire")

ax.plot(xi, yi, marker='+', label='Données expérimentales', linestyle='', color='red')  # On voit l'intérêt des options pour ne pas relier les points

# plt.show()  
""" La ligne précédente a été commentée pour pouvoir tracer ensuite la droite de régression linéaire. 
En pratique, elle permet de vérifier que les points s'alignent à peu près."""

print("L'observation des points de mesure montre effectivement une tendance linéaire")



"""Ajustement linéaire"""
p = np.polyfit(xi, yi, 1)  # p est un vecteur contenant les coefficients.
y_adj = p[0] * xi + p[1]  # On applique la droite ajustée aux xi pour comparaison.

print("--------")
print("La droite ajustée a pour équation :")
print(str(p[0]) + " * x + " + str(p[1]))
print("En pratique, il faudrait tronquer aux bons chiffres significatifs")
print("--------")


ax.plot(xi, y_adj, marker='', label='Ajustement', linestyle='-', color='blue')  # On voit l'intérêt des options

ax.legend()

""" Ce sont des fausses données sans incertitude de mesure, on ne va donc pas comparer le modèle ajusté aux résultats expérimentaux. (cf. exercice)"""

L'observation des points de mesure montre effectivement une tendance linéaire
--------
La droite ajustée a pour équation :
2.353619302949061 * x + 3.6224754244861437
En pratique, il faudrait tronquer aux bons chiffres significatifs
--------

' Ce sont des fausses données sans incertitude de mesure, on ne va donc pas comparer le modèle ajusté aux résultats expérimentaux. (cf. exercice)'
../_images/np_polyfit_3_2.png