Tableaux numpy : manipulations
Contents
Certains points abordés ici serviront très peu ou seront abordés pendant l’année. Il s’agit d’approfondissement pour ceux qui ont déjà bien compris les parties précédentes.
"""On importe les bibliothèques scientifiques car elles seront utilisées ensuite"""
import numpy as np
import matplotlib.pyplot as plt
10. Tableaux numpy : manipulations#
10.1. Opérations usuelles et concaténation#
Les opérations usuelles et fonctions mathématiques présentées précédemment s’appliquent à nouveau pour les tableaux numpy.
Concaténation : La fonction
appenddoit prendre un troisième argument si on concatène deux tableaux (ou un tableau et un vecteur). L’argumentaxis =:axis = 0: Concaténer verticalement : les deux tableaux doivent donc avec le même nombre de colonnes. Sinon Python renverra une erreur.axis = 1: Concaténer horizontalement : les deux tableaux doivent donc avec le même nombre de lignes. Sinon Python renverra une erreur.Pas de
axis: Python va transformer les tableaux en vecteurs et concaténer les vecteurs.
L1 = np.array([[2.3, 2.5], [3.14, 3.16], [3.14, 4.17]])
L2 = np.array([[1.2, 3.7], [4.2, 3.1]])
L3 = np.append(L1, L2) # On aplatit les tableaux pour obtenir un vecteur.
print(L3)
L4 = np.append(L1, L2, axis=0) # On place L2 sous L1
print(L4)
L5 = np.append(L1, L2, axis=1) # Renvoie un erreur car on ne peut placer L2 à droite de L1 : pas le même nombre de lignes
print(L5)
[2.3 2.5 3.14 3.16 3.14 4.17 1.2 3.7 4.2 3.1 ]
[[2.3 2.5 ]
[3.14 3.16]
[3.14 4.17]
[1.2 3.7 ]
[4.2 3.1 ]]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In [2], line 10
7 L4 = np.append(L1, L2, axis=0) # On place L2 sous L1
8 print(L4)
---> 10 L5 = np.append(L1, L2, axis=1) # Renvoie un erreur car on ne peut placer L2 à droite de L1 : pas le même nombre de lignes
11 print(L5)
File <__array_function__ internals>:180, in append(*args, **kwargs)
File D:\cedri\anaconda3\envs\prepa\lib\site-packages\numpy\lib\function_base.py:5444, in append(arr, values, axis)
5442 values = ravel(values)
5443 axis = arr.ndim-1
-> 5444 return concatenate((arr, values), axis=axis)
File <__array_function__ internals>:180, in concatenate(*args, **kwargs)
ValueError: all the input array dimensions for the concatenation axis must match exactly, but along dimension 0, the array at index 0 has size 3 and the array at index 1 has size 2
10.2. Sélection d’une partie d’un tableau.#
Attention
La méthode présentée ne fonctionne pas avec une liste de listes classique. Uniquement avec des tableaux
numpyAttention, l’indexation commence toujours à 0
10.2.1. Sélection d’un élément.#
L1 = np.array([[2.3, 2.5], [3.14, 3.16], [3.14, 4.17]])
print(L1[2, 1])
"""
2 : sélection de la troisième ligne
1 : sélection de la deuxième colonne
On affiche donc 4.17
"""
4.17
'\n2 : sélection de la troisième ligne\n1 : sélection de la deuxième colonne\n\nOn affiche donc 4.17\n'
10.2.2. Sélection d’une portion d’un tableau#
L1 = np.array([[2.3, 2.5, 6.8], [3.14, 3.16, -1.3], [3.14, 4.17, 3.45], [1.6, 4.2, -8.2]])
print("Première sélection", L1[0:2, 1:3]) # Sélection des deux premières lignes (0 et 1) et colonnes d'index (1 et 2). C'est un tableau.
print("Deuxième sélection", L1[:, 1]) # Permet de sélectionner la deuxième colonne en entier (c'est un vecteur)
print("Troisième sélection", L1[1, :]) # Permet de sélectionner la deuxième ligne en entier (c'est un vecteur)
print("Quatrième sélection", L1[1]) # Permet de sélectionner la deuxième ligne en entier aussi (c'est un vecteur)
print("Cinquième sélection", L1[-1, :]) # Permet de sélectionner la dernière ligne en entier (c'est un vecteur)
Première sélection [[ 2.5 6.8 ]
[ 3.16 -1.3 ]]
Deuxième sélection [2.5 3.16 4.17 4.2 ]
Troisième sélection [ 3.14 3.16 -1.3 ]
Quatrième sélection [ 3.14 3.16 -1.3 ]
Cinquième sélection [ 1.6 4.2 -8.2]
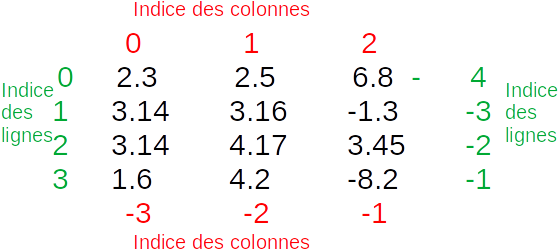
Voici le tableau L1 avec les indices des lignes et colonnes pour mieux comprendre.
10.3. Si j’ai bien compris…#
Exercice
Essayer de prévoir ce qu’affichera chaque print puis observer le résultat en cliquant sur la croix en bas à droite.
L1 = np.arange(0, 4)
L2 = L1 * L1
L3 = np.ones(4)
"""
Ci-dessous : une méthode pour créer un tableau à partir de 3 vecteurs de même taille.
Les L1, L2, L3 sont les lignes du tableau.
"""
M1 = np.array([L1, L2, L3])
print("Cas 1 :", M1)
print("Cas 2 :", M1[2, 3])
print("Cas 3 :", M1[-1, 2])
print("Cas 4 :", M1[1])
print("Cas 5 :", M1[2, :])
print("Cas 6 :", M1[:, -1])
print("Cas 7 :", M1[:, -2])
print("Cas 8 :", M1[1:2, 0:1])
print("Cas 9 :", M1[:-1, 1]) # Un peu plus compliqué...
print("Cas 10 :", M1[-3:-1, -3:3]) # On se concentre bien...
Cas 1 : [[0. 1. 2. 3.]
[0. 1. 4. 9.]
[1. 1. 1. 1.]]
Cas 2 : 1.0
Cas 3 : 1.0
Cas 4 : [0. 1. 4. 9.]
Cas 5 : [1. 1. 1. 1.]
Cas 6 : [3. 9. 1.]
Cas 7 : [2. 4. 1.]
Cas 8 : [[0.]]
Cas 9 : [1. 1.]
Cas 10 : [[1. 2.]
[1. 4.]]
Explication des réponses
Les vecteurs :
L1 crée une liste d’entier partant de 0 jusqu’à 4 exclus soit
[0, 1, 2, 3]L2 est la multiplication terme à terme L1 par lui-même, on passe chaque élément au carré soit
[0, 1, 4, 9]L3 est une liste de 4 éléments composées uniquement de 1.
Le tableau :
M est le tableau composé des trois vecteurs. Il est donc de taille 3*4 (3 lignes, 4 colonnes). Soit :

Les affichage:
Cas 1 : Affichage du tableau complet
Cas 2 : Affichage de l’élément de la troisième ligne (indice 2), quatrième colonne (indice 3), soit
1.0Cas 3 : Afficahge de l’élément de la dernière ligne (indice -1), troisième colonne (indice 2) soit
1.0Cas 4 : Affichage de la deuxième ligne (indice 1) soit
array([0., 1., 4., 9.])Cas 5 : Affichage de la troisième ligne (indice 2) soit
array([1., 1., 1., 1.])Cas 6 : Affichage de la dernière colonne (indice -1) soit
array([3., 9., 1.])Cas 7 : Affichage de l’avant-dernière colonne (indice -2) soit
array([2., 4., 1.])Cas 8 : Affichage du tableau limité à la deuxième ligne (de l’indice 1 à l’indice 2 exclus) et à la première colonne soit
array([[0.]])(de l’indice 0 à l’indice 1 exclus). C’est bien un tableau mais avec une seule valeur !Cas 9 : Affichage de la deuxième colonne mais sans la dernière ligne (on va jusqu’au -1 exclus)
array([1., 1.])Cas 10 : Affichage du tableau limité aux deux premières lignes (de l’indice -3 soit indice 0 - puisqu’il y a 3 lignes - jusqu’à l’indice -1 (dernier) exclus) et à la deuxième et troisième colonne (de l’indice - 3 soit la colonne d’indice 1 - puisque qu’il y a 4 colonnes - jusqu’à l’indice 3 soit la dernière colonne exclus) soit
array([[1., 2.], [1., 4.]])

