4. S’entraîner (Import et tirages aléatoires)#

La partie donnant les concepts pour faire ces exercices est accessible ici.

Important

Une partie des exercices suivants utilisent des données expérimentales stockées dans des fichiers. Chaque exercice vous donnera le lien permettant de télécharger le fichier. Vous avez normalement créé un répertoire pour votre travail sous Python. Dans ce répertoire (ou le sous-répertoire où vous comptez créer vos fichier .py pour les exercices, créez un répertoire donnees_exp dans lesquelles vous téléchargerez les fichiers fournis.

Vous devrez ensuite réfléchir au chemin relatif à utiliser dans vos scripts pour importer les données expérimentales de ces fichiers.

4.1. Utilisation de numpy.random#

Utilisation de numpy.random

Vous devez :

Importer la sous-bibliothèque numpy.random dans l’espace nommé rd pour l’utiliser ensuite.
Utiliser la fonction uniform pour créer un vecteur contenant \(N = 1000000\) de tirages aléatoires entre 0 et 5.
Obtenir alors le vecteur X contenant le carré de chaque valeur tirée précédemment.
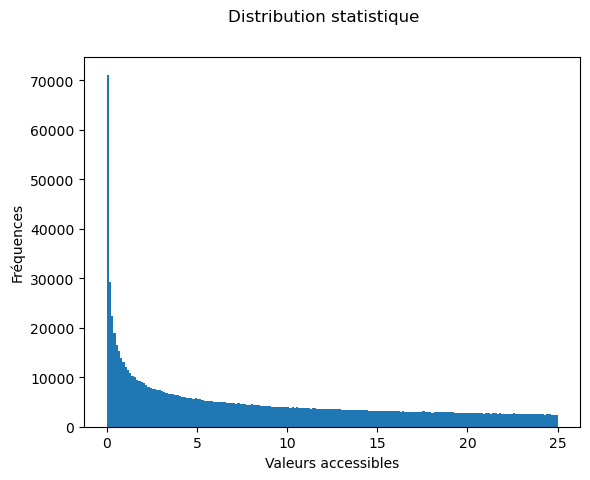
Tracer l’histogramme des valeurs de X. Le titre sera “Distribution statistique”, il n’est pas utile d’afficher la légende.

Vous devriez obtenir le graphique suivant (Cliquez sur la croix. Cela peut un peu varier puisqu’on fait des tirages aléatoires) :

import matplotlib.pyplot  as plt
import numpy as np
import numpy.random as rd

N = 1000000

x = rd.uniform(0, 5, N)
X = x * x

f, ax = plt.subplots()
f.suptitle("Distribution statistique")

ax.set_xlabel("Valeurs accessibles")
ax.set_ylabel("Fréquences")

ax.hist(X, bins='rice')

plt.show()

4.2. Etude de données expérimentales#

Etude de données expérimentales

On étudie un circuit RC en régime libre. On a pris \(R = 100k\Omega\) et on veut mesurer la capacité \(C\) grâce aux données expérimentales. Les données sont fournies dans le fichier circuit_rc_decharge.dat accessible par ce lien.

Note

Si votre navigateur ouvre le fichier au lieu de le télécharger, faites un clic droit sur le lien et choisir Enregistrer la cible du lien)

Pour rappel, la tension \(u_c\) aux bornes du condensateur est régit par l’équation différentielle :

\[ \frac{\rm{d}u_c}{\rm{dt}} + \frac{u_c}{RC} = 0 \]

Il a pour solution :

\[ u_c(t) = U_0 \exp(-\frac{t}{\tau}) \]

avec \(\tau = RC\) et \(U_0 = U(t=0)\)

On sait que \(u_c(t > \tau) < 0.37 U_0\).

Après avoir téléchargé le fichier de données et l’avoir déplacé dans le répertoire donnees_exp, l’ouvrir dans pyzo et observer son contenu. Quelles données expérimentales contient-il ?
Créer un fichier script Python (faire attention à sa localisation) et commencer par y importer les bibliothèques numpy et matplotlib.pyplot. Ecrire ensuite les instructions important la colonne temps et la colonne tension (en binaire) dans deux vecteurs temps et ucb.
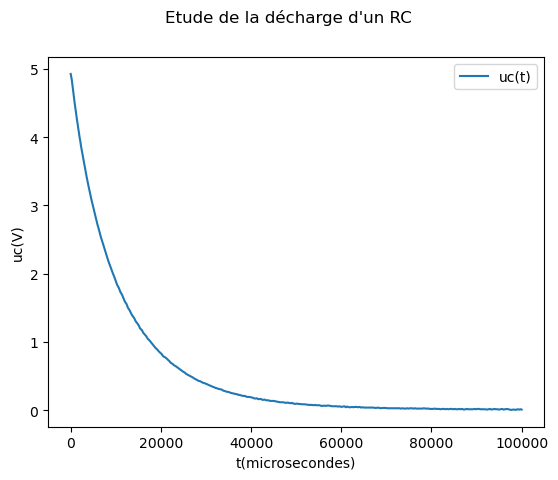
La tension n’est pas données en volt mais est un nombre entier : l’équivalent décimal de sa représentation binaire. En vous servant de la description données dans le fichier de données, écrire une fonction bin_to_volt qui prend comme argument une valeur b en binaire et qui renvoie la valeur de tension correspondant en Volt. Utilisez la pour obtenir un vecteur numpy uc à partir de ucb
Représenter, sur un graphique légendé et titré la courbe \(u_c(t)\). L’allure est-elle conforme (visuellement) aux attentes théoriques ?
En utilisant les informations données dans l’énoncé, écrire une fonction estime_tau qui prend en argument deux vecteurs numpy t et u et qui estime le temps tau. On admettra que \(u(t)\) est bien décroissante et on pourra prendre la première valeur de \(u\) comme valeur de \(U_0\). Utiliser cette fonction pour obtenir une estimation de \(\tau\) puis de \(C\).

"""Les libraires ont déjà été importées à l'exercice précédent"""
temps, ucb = np.loadtxt('Sf6/circuit_rc.dat', skiprows=7, delimiter=";", unpack=True)  # Importation des données

def bin_to_volt(u):
	"""Fonction qui transforme une valeur 0-255 en valeur de tension."""
	B_MAX = 1023
	U_MAX = 5
	B_MIN = 0
	U_MIN = 0
	tension = (u - B_MIN) / (B_MAX - B_MIN) * (U_MAX - U_MIN) + U_MIN
	return tension

uc = bin_to_volt(ucb)


"""Tracé de uc(t)"""
f, ax = plt.subplots()
f.suptitle("Etude de la décharge d'un RC")
ax.set_xlabel('t(microsecondes)')
ax.set_ylabel('uc(V)')

ax.plot(temps, uc, label='uc(t)')

ax.legend()
plt.show()

"""Détermination de tau"""
U0 = uc[0]  # Tension initiale
i = 0
while uc[i] > 0.37 * U0 and i < len(uc):  # Test des 37%
    i = i + 1
print(temps[i])  # Temps juste avant d'invalider la condition
print(temps[i+1])  # Temps juste après invalidation

tau = (temps[i] + temps[i+1]) / 2  # On prend la moyenne des deux
R = 1e5  # Valeur de R
C = tau / R / 1e6  # (tau était en microsecondes)

print("Valeur estimée de tau :", tau)
print("Valeur estimée de C :", C)
print("Tous les chiffres ne sont pas forcément significatifs...")

10700.0
11000.0
Valeur estimée de tau : 10850.0
Valeur estimée de C : 1.085e-07
Tous les chiffres ne sont pas forcément significatifs...

4.3. Expériences multiples#

Expériences multiples

On reprend l’exemple précédent (même valeurs de R et C) mais cette fois le montage réalisé au moyen d’un microcontrolleur Arduino a permis d’automatiser la mesure de la constante \(\tau\). On a ainsi réalisé \(N\) décharges de C et le microcontrolleur a été programmé pour mesurer à chaque fois \(\tau\) et le transmettre à l’ordinateur. Un programme non présenté ici a stocké les valeurs de \(\tau\) dans un fichier accessible à ce lien.

Note

Si votre navigateur ouvre le fichier au lieu de le télécharger, faites un clic droit sur le lien et choisir Enregistrer la cible du lien)

Après avoir téléchargé le fichier de données et l’avoir déplacé dans le répertoire donnees_exp, l’ouvrir dans pyzo et observer son contenu. Quelles données expérimentales contient-il ?
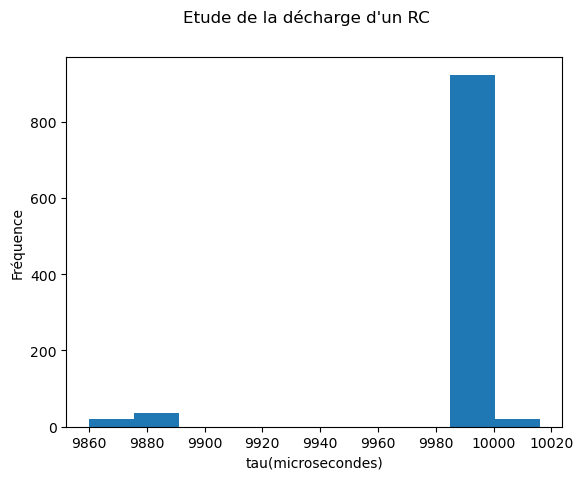
Créer un fichier script Python (faire attention à sa localisation) et commencer par y importer les bibliothèques numpy et matplotlib.pyplot. Ecrire ensuite les instructions important la colonne tau dans un vecteur taus. Afficher ensuite en une seule instruction la valeur du nombre N de décharges qui ont été réalisées.
Créer un graphique représentant l’histogramme des valeurs de \(\tau\) mesurées. Observe-t-on des valeurs assurément problèmatiques ?
Utiliser les fonctions de numpy pour estimer la valeur moyennes des mesures de \(\tau\) ainsi que l’écart-type des mesures. Utiliser la valeur moyenne de \(\tau\) pour obtenir une estimation de la capacitance \(C\).

taus = np.loadtxt('Sf6/circuit_rc_auto.dat', skiprows=7, delimiter=",")  # Importation des données


print("Nombre de mesures :", len(taus))

f, ax = plt.subplots()
f.suptitle("Etude de la décharge d'un RC")
ax.set_xlabel('tau(microsecondes)')
ax.set_ylabel('Fréquence')

ax.hist(taus)

plt.show()

"""Calcul de la moyenne et écart-type"""
tau_m = np.mean(taus)
tau_u = np.std(taus, ddof=1)

print("Tau moyen : ", tau_m)
print("Ecart-type : ", tau_u)
print("Tous les chiffres ne sont pas forcément significatifs...")

R = 1e5  # Valeur de R
C = tau_m / R / 1e6  # (tau était en microsecondes)
print("Valeur estimée de C :", C)

Nombre de mesures : 1000

Tau moyen :  9985.208
Ecart-type :  27.001144379410995
Tous les chiffres ne sont pas forcément significatifs...
Valeur estimée de C : 9.985208000000001e-08

4.4. Célérité des ultrasons#

Cet exercice est un peu plus complet. Veillez à bien comprendre ce qui a été fait précédemment.

Célérité des ultrasons

Le but est d’étudier la propagation des ultrasons dans l’air pour estimer leur célérité. Grâce à un microcontrolleur (Arduino), on a réalisé un grand nombre de mesures (environ 1000) du temps de vol \(\Delta t\) des ultrasons pour plusieurs distances différentes \(2d\) (on a réalisé un aller-retour par réflexion sur un obstacle) afin d’estimer pour chaque distance la célérité moyenne \(c = {2d \over \Delta t(d)}\). On fera alors la moyenne des célérités sur toutes les distances pour estimer la célérité des ultrasons dans l’air.

Le fichier de données est à télécharger à ce lien.

Note

Si votre navigateur ouvre le fichier au lieu de le télécharger, faites un clic droit sur le lien et choisir Enregistrer la cible du lien)

Après avoir téléchargé le fichier de données et l’avoir déplacé dans le répertoire donnees_exp, l’ouvrir dans pyzo et observer son contenu. Quelles données expérimentales contient-il ? (Les temps de vol sont données en microsecondes).
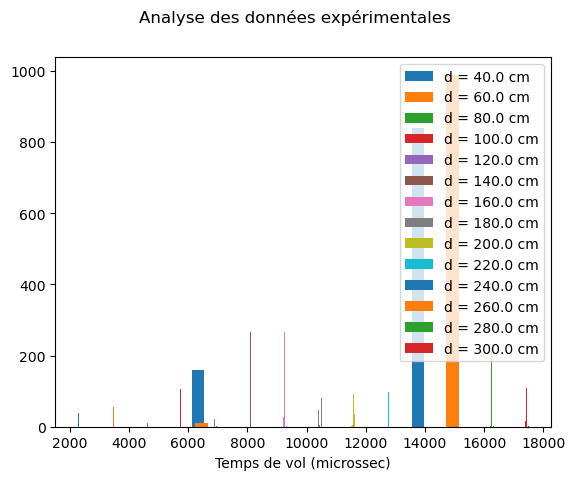
Vous avez dû remarquer que la forme du tableau de données n’est pas comme les précédents. Importer le tableau complet dans une variable donnees. On traitera dans une boucle les données pour chaque distance.
Créer un graphique et y tracer, pour chaque distance l’histogramme des valeurs mesurées. On prendra soin de bien légender chaque histogramme par sa distance. Vous DEVEZ utiliser une boucle qui puisse s’adapter à un autre fichier de données qui aurait la même forme mais pas forcément les mêmes distances (ni le même nombre de distances étudiées). Quelques informations utiles sont données à la fin de l’exercice.
Observer les histogrammes, vous devriez observer que certaines mesures sont clairement aberrantes. Nous allons proposées une méthode de sélection des valeurs acceptables.

La méthode de sélection (non expliquée ici) consiste à calculer la moyenne \(\Delta t_m (d)\) et l’écart-type \(\sigma (d)\) des valeurs de temps de vol pour une distance \(d\) puis parcourir l’ensemble des valeurs mesurées \(\Delta t_i (d)\) pour la distance \(d\).

Si l’écart à la moyenne \(\left\vert (\Delta t_i (d) - \Delta t_m (d) \right\vert\) est inférieure à 2 écart-type (\(2 \sigma (d)\)), alors on garde la valeur.
Si l’écart à la moyenne \(\left\vert (\Delta t_i (d) - \Delta t_m (d) \right\vert\) est supérieure à 2 écart-type (\(2 \sigma (d)\)), alors on enlève la valeur.

Ecrire une fonction qui prend comme argument un vecteur numpy u et qui renvoie un vecteur numpy u_sel ne contenant que les valeurs acceptables.
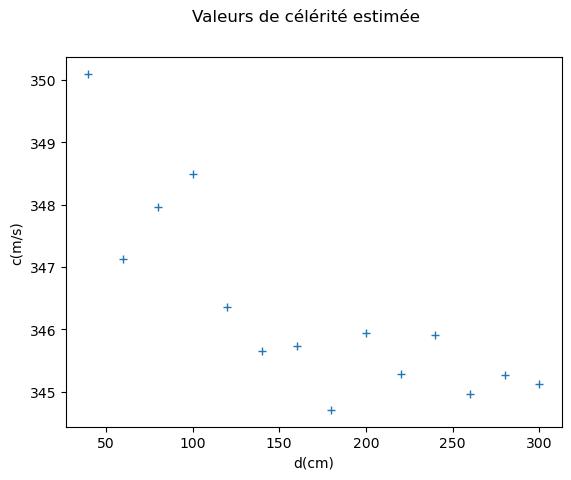
Pour chaque distance \(D\) (toujours avec la contrainte de devoir s’adapter à un autre fichier de mesure), sélectionner les valeurs à garder puis calculer le temps de vol moyen puis la célérité du son associée \(c(d)\). Stocker cette célérité dans un vecteur numpy cs.
Représenter les valeurs des célérités estimées en fonction de \(D\) et vérifier qu’on observe bien à peu près la même valeur pour distance (on ne peut faire mieux qu’une estimation visuelle sans la données des incertitudes).
Estimer la moyenne de cs comme une estimation de la célérité des ultrasons. Sachant qu’elle est à peu près identique à la célérité du son dans l’air, vérifier si l’ordre de grandeur obtenu est correct. Sans estimation des incertitudes de mesures, on se limitera à une vérification de l’ordre de grandeur.

Compléments utiles:

L’option label ne prend comme argument qu’une chaine de caractère. Vous pouvez transformer un flottant ou un entier en chaine de caractère x par str(x). Vous pouvez aussi concaténer cette chain avec d’autres : str(x) + " cm".

donnees = np.loadtxt('Sf6/vitesse_son_2.dat', skiprows=10, delimiter=",")
distances = donnees[:, 0]  # Récupération des distances.

"""Tracé des histogrammes"""
f, ax = plt.subplots()
f.suptitle("Analyse des données expérimentales")
ax.set_xlabel("Temps de vol (microssec)")

for data in donnees:
    d = data[0]  # Distance d'étude
    tps = data[1:]  # Les temps de vol
    ax.hist(tps, bins='rice', label="d = " + str(d) + " cm")  # Tracé de l'histogramme. Observer l'ajout de la légende.

ax.legend()

plt.show()

def selection(u):
    """Fonction qui sélectionne les valeurs acceptables du vecteur u"""
    um = np.mean(u)  # Calcul de la moyenne
    uu = np.std(u, ddof=1)  # Calcul de l'écart-type

    """Important : On ne connait pas quelle va être la taille de u_sel.
    L'usage d'un vecteur numpy est donc déconseillé. On va créer une liste classique
    qu'on transformera à la fin en vecteur numpy.
    """
    u_sel = []  # Liste où l'on va stocker les valeurs sélectionnées.
    for val in u:  # On parcourt les valeurs de la liste.
        if np.abs(val - um) <= 2 * uu:  # Test d'écart à la valeur moyenne
            u_sel.append(val)  # On ajoute la valeur
    return np.array(u_sel)  # On transforme u_sel en vecteur numpy


"""Détermination des valeurs de c"""
cs = []  # Liste pour les célérités
for data in donnees:
    d = data[0]  # Distance
    t_sel = selection(data[1:])  # Sélection des valeurs acceptables
    t_moy = np.mean(t_sel)
    c = 2 * d / t_moy
    cs.append(c)

cs = np.array(cs) / 100 * 1000000  # On passe à des m/s

f, ax = plt.subplots()
f.suptitle("Valeurs de célérité estimée")
ax.set_xlabel("d(cm)")
ax.set_ylabel("c(m/s)")

ax.plot(distances, cs, label="Célérité", marker='+', linestyle='')  # On ne relie pas les points.

print("On observe des valeurs entre 345m/s et 350m/s soit des valeurs peu dispersées.")
plt.show()  # Pensez à commenter le précédent plt.show()

On observe des valeurs entre 345m/s et 350m/s soit des valeurs peu dispersées.

celerite = np.mean(cs)

print("---------")
print("Valeur estimée de la célérité :")
print(str(celerite) + "m/s")
print("---------")

---------
Valeur estimée de la célérité :
346.3315935386808m/s
---------

Python : Bases à connaître - Exercice

S’entraîner (Import et tirages aléatoires)

Contents

4. S’entraîner (Import et tirages aléatoires)#

4.1. Utilisation de numpy.random#

4.2. Etude de données expérimentales#

4.3. Expériences multiples#

4.4. Célérité des ultrasons#