S’entraîner.
Contents
2. S’entraîner.#
La partie donnant les concepts pour faire ces exercices est accessible ici.
Voici quelques exercices pour vous entraîner à coder. Les conseils donnés pour les premiers exercices sont toujours valables. Pensez à créer un fichier par exercice.
2.1. Tracé simple.#
Tracé simple.
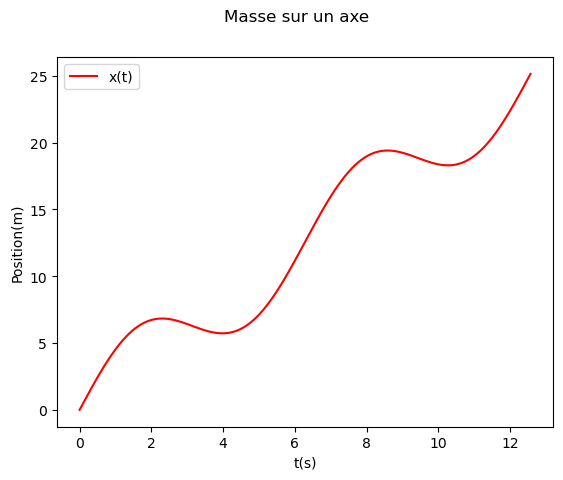
Vous devez tracer le graphique de la fonction \(f(x) = 2x + 3 * sin(x)\) sur l’intervalle \([0, 4\pi]\) en prenant \(N = 2000\) points pour le tracé.
On suppose qu’il s’agit du mouvement d’une “Masse sur un axe”. Le tracé de la courbe devra être rouge (trait plein). Les abscisses seront des temps (en secondes) et les ordonnées des positions (en mètre). Utilisez ces informations pour légender et titrer votre graphique.
Quelques indices pour s’organiser
Vous avez besoin des deux bibliothèques. N’oubliez pas de les importer.
Vous n’allez pas créer un vecteur de 2000 points manuellement, pensez aux fonction qui permettent de créer automatiquement des vecteurs.
Seule la fonction
sinde la bibliothèquenumpyest vectorialisable.Essayer d’avoir une organisation claire de vos instructions pour créer le graphique. Vous pourrez la réutiliser souvent.
Vous devriez obtenir le graphique suivant (cliquez sur la croix).
import matplotlib.pyplot as plt
import numpy as np
def f(x):
return 2*x + 3 *np.sin(x)
x = np.linspace(0, 4 * np.pi, 2000)
y = f(x)
f, ax = plt.subplots()
f.suptitle("Masse sur un axe")
ax.set_xlabel("t(s)")
ax.set_ylabel("Position(m)")
ax.plot(x, y, color='red', label='x(t)')
ax.legend()
<matplotlib.legend.Legend at 0x1b11224ecd0>
2.2. Tracé et manipulation des vecteurs#
Tracé et manipulation des vecteurs
Un point matériel M de masse \(m\) se déplaçant sans frottements sur un axe \(Ox\) en étant attaché à un ressort de raideur \(k\) et de longueur à vide \(l_0\) constitue un oscillateur harmonique. L’évolution temporelle de la position du point M (lâché depuis la position \(X_0\) sans vitesse initiale) est donnée par :
avec \(\omega_0 = \sqrt{\frac{k}{m}}\)
Montrer par le calcul que la vitesse du point M est donnée par \(v_M(t) = -(X_0 - l_0) \omega_0 \sin (\omega_0 t)\).
Vous devez créer quatre graphiques :
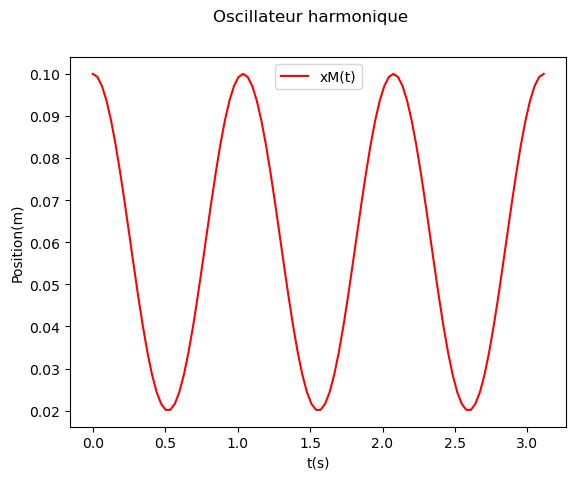
Le premier représente la position \(x_M\) en fonction du temps.
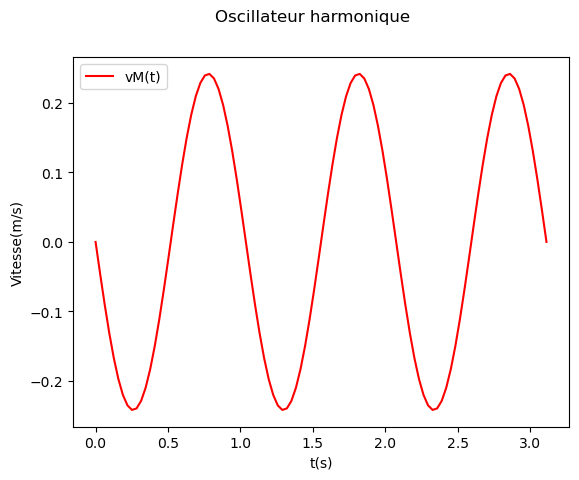
Le second représente la vitesse \(v_M\) en fonction du temps.
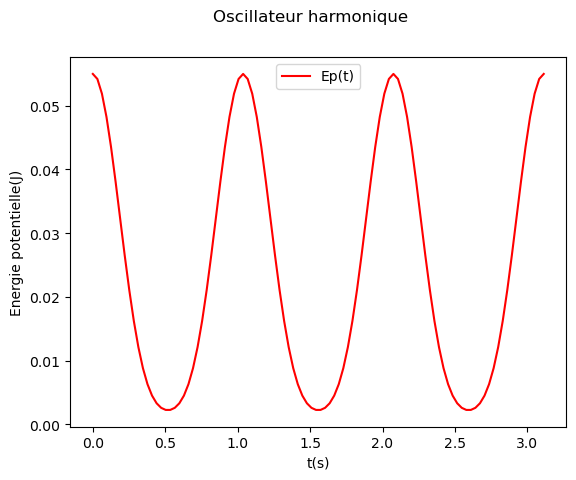
Le troisième représente l’énergie potentielle \(E_p = \frac{1}{2}k x_M^2\) en fonction du temps.
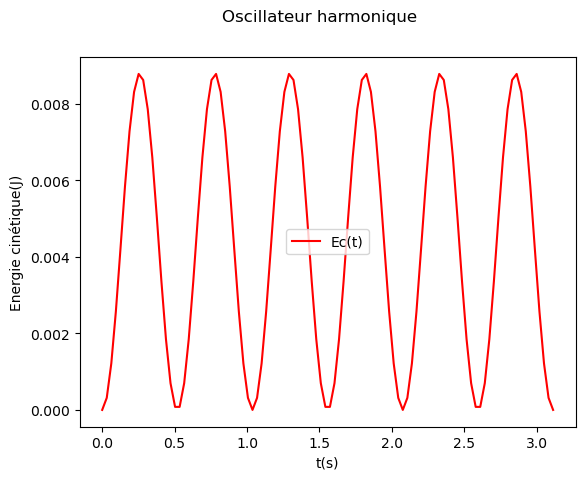
Le quatrième représente l’énergie cinétique \(E_c = \frac{1}{2}m v_M^2\) en fonction du temps.
On prendra : \(k=11 \rm{N.m^{-1}}; m=0.3 \rm{kg}; X_0 = 0.1 \rm{m}; l_0=0.06 \rm{m}\) et on réfléchira au vecteur numpy temps à créer pour calculer les abcisses. Il faut :
observer suffisamment de périodes (3)
suivre les variations du signal (une centaine de points par période)
N’oubliez le caractère vectoriel des opérations sur les vecteurs numpy, vous devez écrire ce script sans utiliser de boucle. Cliquez sur la croix pour voir ce que vous devez obtenir.
k = 11
m = 0.3
X0 = 0.1
l0 = 0.06
w0 = np.sqrt(11 / 0.3)
def xM(x):
return (X0 - l0) * np.cos(w0 * x) + l0
def vM(x):
return - w0 *(X0 - l0) * np.sin(w0 * x)
temps = np.linspace(0, 6 * np.pi / w0, 100)
xMt = xM(temps)
vMt = vM(temps)
Ep = 1 / 2 * k * xMt ** 2
Ec = 1 / 2 * m * vMt ** 2
f, ax = plt.subplots()
f.suptitle("Oscillateur harmonique")
ax.set_xlabel("t(s)")
ax.set_ylabel("Position(m)")
ax.plot(temps, xMt, color='red', label='xM(t)')
ax.legend()
f, ax = plt.subplots()
f.suptitle("Oscillateur harmonique")
ax.set_xlabel("t(s)")
ax.set_ylabel("Vitesse(m/s)")
ax.plot(temps, vMt, color='red', label='vM(t)')
ax.legend()
f, ax = plt.subplots()
f.suptitle("Oscillateur harmonique")
ax.set_xlabel("t(s)")
ax.set_ylabel("Energie potentielle(J)")
ax.plot(temps, Ep, color='red', label='Ep(t)')
ax.legend()
f, ax = plt.subplots()
f.suptitle("Oscillateur harmonique")
ax.set_xlabel("t(s)")
ax.set_ylabel("Energie cinétique(J)")
ax.plot(temps, Ec, color='red', label='Ec(t)')
ax.legend()
<matplotlib.legend.Legend at 0x1b1123ee130>