2. (TP) Application à l’étude des ultrasons. (1h)#

On reprend l’étude de la propagation des ultrasons. Le but est de déterminer la célérité du son dans l’air. Le protocole réalisé et le matériel utilisé est celui proposé dans l’exercice que vous avez fait précédemment.

2.1. Réalisation du protocole et estimation des incertitudes-type#

Cette partie sera réalisée en TP. Lisez-là pour savoir ce que vous devrez faire mais vous ne pourrez pas faire grand chose avant le TP (sauf précision).

2.1.1. Mise en place#

Le protocole à réaliser est affichable en cliquant sur la croix à droite.

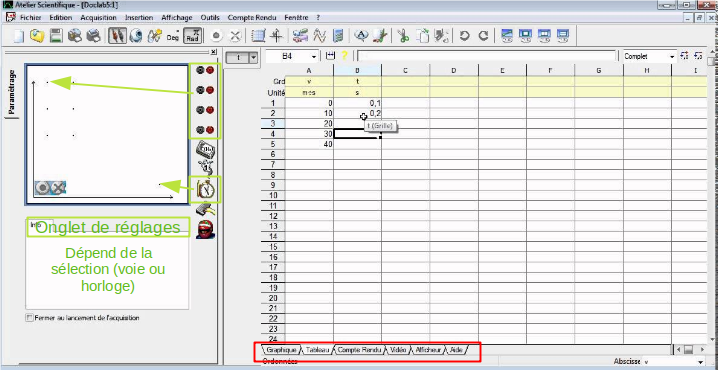
Fig. 2.1 Titre#

Réaliser le montage en n’oubliant pas d’alimenter l’émetteur et de le régler et en branchant les deux récepteurs sur la console FOXY. Régler l’émetteur en mode salves courtes.
Brancher un connecteur BNC-fil simple entre l’émetteur et FOXY. Ce signal est le signal alimentant l’émetteur (pas le signal émis). Il servira à synchroniser l’affichage.
Brancher la console FOXY à l’ordinateur. Une “tablette” simulée s’ouvre. Choisir généraliste.
Préparer l’acquisition (Affichage > Acquisition Conseil : décocher l’option “Fermer au lancement de l’acquisition” pour garder cette fenêtre de réglage durant le TP):
- Choisir les voies à acquérir (icone rouge et noir à droite du mini-graphique)
  1. Les placer (glisser-déplacer) sur l’axe des ordonnées du petit graphique.
  2. Les nommer clairement (onglet Grandeur sous le petit graphique quand vous sélectionner la voie choisie)
  3. Choisir le calibre de chaque voie (le signal ne dépassera pas 10V).
- Régler la base de temps de l’acquisition
  1. Choisir d’acquérir en fonction du temps (Horloge à placer sur l’axe des abscisses)
  2. Régler la durée d’acquisition (dans Fonction du temps quand vous sélectionnez l’horloge) comme choisi dans l’étude préliminaire.
  3. Régler le nombre de points à 10000 (on apprendra plus tard à réfléchir à ce choix).
  4. Cocher Acquisition continue de manière à ne pas avoir besoin de relancer l’acquisition à chaque fois.
- Régler la synchronisation : il faut choisir à quelle valeur démarrera l’affichage des signaux pour observer un signal stable.
  1. Dans l’onglet (Menus de l’horloge) Synchronisation choisir la Voie de synchro correspondant au signal de l’émetteur.
  2. Choisir une Niveau de 1(V) Croissant.
- Vous pouvez maintenant lancer l’acquisition !

2.1.2. Réalisation des mesures - Bilan des incertitudes#

Vous devez maintenant réaliser la mesure.

Attention

Au préalable, vous avez dû discuter au préalable avec le reste du groupe pour vous répartir les distances de mesure de sorte que chaque élève fasse une mesure de temps de vol pour une distance différente.

Rendre compte :

des résultats de mesurage
des différentes sources d’incertitude avec leur estimation si elles sont non négligeables

2.2. Estimation de la célérité.#

2.2.1. Estimation simple#

Vous aller devoir utiliser la cellule suivante pour déterminer la célérité. On ne s’occupe pas pour l’instant de déterminer son incertitude.

"""
Vous devez commencer par importer les bibliothèques utiles :
- numpy (manipulation de vecteurs de valeurs)
- numpy.random (simulation de tirages aléatoires)
- matplotlib.pyplot (tracés graphiques)
Elles seront utiles par la suite (pas pour cette cellule).
"""
import numpy as np  # Pour le calcul sur un ensemble de valeurs
import numpy.random as rd  # Pour la création de nombres aléatoires
import matplotlib.pyplot as plt  # Pour les tracés graphiques

"""
Il faudra bien sûr modifier cette partie en TP.

Enregistrer les valeurs mesurées dans des variables t1_m, t2_m, d1_m et d2_m
"""
N = 1000000  # Nombre de simulations
t1_m = 34  # Valeur mesurée pour t1
t2_m = 0  # Valeur mesurée pour t2
d1_m = 0  # Valeur mesurée pour d1
d2_m = 0  # Valeur mesurée pour d2


# Estimation de la célérité
c_m = 0  # Utiliser LES VARIABLES introduites précédemment pour estimer la célérité des ondes.

print("c = " + str(c_m))  # ATTENTION : Les chiffres ne sont évidemment pas tous significatifs.

2.2.2. Combinaison des incertitudes. Simulation de Monte-Carlo.#

Pour rappel, la méthode de Monte-Carlo consiste:

On répète N fois:
1. à simuler de nouvelles valeurs des mesurandes directes (ici \(t_1, t_2, d_1, d_2\)) : on réalise, pour chaque source d’incertitude un tirage aléatoire d’une valeur suivant la distribution choisie (ici des distributions uniformes de largeur estimée lors de l’expérience - numpy.random.uniform(a : float, b :float) -> float) auquel on ajoute la valeur mesurée (t1_m, t2_m, d1_m, d2_m).
2. à déterminer une nouvelle valeur simulée du mesurandes indirect recherché (ici \(c\)) et stocker cette valeur dans une liste prévue au préalable.
On obtient ainsi une liste de N valeurs de \(c\) simulées à partir des tirages aléatoires. On peut donc calculer des grandeurs statistiques. On calculera ainsi:
1. L’écart-type (numpy.std(liste_val : list, ddof=1) -> float)de la liste de valeurs et on considèrera cet ecart-type comme étant l’incertitude sur \(c\).

2.2.2.1. Monte-Carlo : Méthode 1#

La première méthode est la plus simple à comprendre et à mettre en oeuvre. Elle présente par contre le plus long temps d’exécution.

Note: La ligne %time permet simplement d’afficher le temps de calcul de la cellule entière.

%time
"""
Il faut d'abord rentrer les DEMIE-LARGEURS des distributions pour chaque sources d'incertitude de chaque grandeur.
- S'il y a moins de sources d'incertitude, supprimez en.
- S'il y a plus de sources d'incertitude, ajoutez en en vous aidant du modèle.
"""
# Incertitudes estimées
# sur t1 --- 
t1_u1u = 0.3  # Demie-largeur de la première source d'incertitude de t1
t1_u2u = 0.1  # Demie-largeur de la deuxième source d'incertitude de t1

# sur t2 ---



# sur  d1 ---



# sur d2 ---



# INITIALISATION
N = 100000  # Nombre de simulations réalisées.
c_sim = []  # Liste vide où on va stocker les valeurs

for i in range(N):
    """
    On reprend le même code que pour calculer une valeur de c.
    Sauf que les valeur de t1, t2, ... sont légèrement modifiées par un tirage aléatoires
    pour CHAQUE sources d'incertitudes.
    """
    # MODIFIER ces lignes en fonction du nombre de sources d'incertitudes estimées précédemment.
    t1_sim = t1_m + rd.uniform(-t1_u1u, t1_u1u) + rd.uniform(-t1_u2u, t1_u2u)
    t2_sim = t2_m
    d1_sim = d1_m
    d2_sim = d2_m 

    c = 0 # A modifier en le calcul comme précédemment (mais avec les t1_sim,...)

    c_sim.append(c)  # On stocke la valeur simulées

"""
Estimation de l'incertitude de mesure
"""
c_u = np.std(c_sim, ddof=1)

print("u(c) = " + str(c_u))

2.2.2.2. Monte-Carlo : Méthode 2#

La deuxième méthode conserve l’idée de l’itération précédente mais elle va créer les N valeurs simulées des mesurandes directes (ici \(t_1, t_2, d_1, d_2\)) d’un seul coup AVANT la boucle. On ira piocher dans les listes ainsi créées. L’avantage est que la création des N valeurs est beaucoup plus rapide. Il suffit de rajouter un troisième argument optionnel : numpy.random.uniform(a: float, b: float, N: int) -> ndarray. On obtient alors un vecteur numpy (ndarray) et non une seule valeur.

%time
"""
Il n'est pas utile de redéfinir les incertitudes t1_u1u...
Si vous avez exécuté le bloc précédent, elles sont en mémoire.
"""

# INITIALISATION
N = 100000  # Nombre de simulations réalisées.
c_sim = []  # Liste vide où on va stocker les valeurs

# On simule ici N valeurs d'un seul coup pour chaque mesurandes directs.
# MODIFIER les différentes lignes pour l'adapter aux exemples ici.
t1_sims = t1_m + rd.uniform(-t1_u1u, t1_u1u, N) + rd.uniform(-t1_u2u, t1_u2u, N)
t2_sims = t2_m
d1_sims = d1_m
d2_sims = d2_m 

for i in range(N):
    """
    On reprend le même code que pour calculer une valeur de c.
    Sauf qu'on ne refait par le tirage aléatoire, on pioche juste dans les valeurs déjà simulées.
    """
    # MODIFIER ces lignes en vous aidant de la première.
    t1_sim = t1_sims[i]
    t2_sim = t2_m
    d1_sim = d1_m
    d2_sim = d2_m 

    c = 0 # A modifier en le calcul comme précédemment (mais avec les t1_sim,...)

    c_sim.append(c)  # On stocke la valeur simulées

"""
Estimation de l'incertitude de mesure
"""
c_u = np.std(c_sim, ddof=1)

print("u(c) = " + str(c_u))

2.2.2.3. Monte-Carlo : Méthode 3#

On peut encore gagner du temps en utilisant la vectorialisation. En effet, les opérations pour obtenir \(c\) (soustractions et division) peut s’appliquer directement entre deux vecteurs numpy terme à terme.

%time
"""
Il n'est pas utile de redéfinir les incertitudes t1_u1u...
Si vous avez exécuté le bloc précédent, elles sont en mémoire.
"""



# INITIALISATION
N = 100000  # Nombre de simulations réalisées.
c_sim = []  # Liste vide où on va stocker les valeurs

# On simule ici N valeurs d'un seul coup pour chaque mesurandes directs.
# MODIFIER les différentes lignes pour l'adapter aux exemples ici.
t1_sims = t1_m + rd.uniform(-t1_u1u, t1_u1u, N) + rd.uniform(-t1_u2u, t1_u2u, N)
t2_sims = t2_m
d1_sims = d1_m
d2_sims = d2_m 

# MODIFIER la ligne ci après en utilisant t1_sims, t2_sims... comme si c'était de simple flottants.
# Comme ce sont des vecteurs numpy, la vectorialisation appliquera la relation mathématiques terme à terme : c_sim est un vecteur.
c_sim = 0
print(type(c_sim))  # Observer en sortie que c_sim est bien un vecteur de taille N


"""
Estimation de l'incertitude de mesure
"""
c_u = np.std(c_sim, ddof=1)

print("u(c) = " + str(c_u))

Cette dernière méthode, BEAUCOUP PLUS RAPIDE, peut s’appliquer tant que les opérations mises en jeu sont vectorialisables par numpy soit:

+,-,/,*
les fonctions usuelles numpy.sin, numpy.cos, numpy.tan, numpy.log, numpy.exp... à condition qu’elle proviennent de la bibliothèqe numpy et non la bibliothèque math.

Exception notoire:

numpy.polyfit qui permet de faire des régression linéaire n’est pas vectorialisable.

2.2.2.4. Autre avantage des méthodes 2 et 3#

On obtient par ces méthodes une liste (vecteur pour être précis) de valeurs simulées aussi pour \(t_1, t_2...\)^. On peut donc aussi calculer l’incertitude-type pour ces grandeurs et donc en rendre-compte dans son compte-rendu. Ici:

# MODIFIER les lignes suivantes en s'inspirant de la première
t1_u = np.std(t1_sims, ddof=1)  # Incertitude sur t1
t2_u = 0
d1_u = 0
d2_u = 0


print("t1 = {} +/- {}".format(t1_m, t1_u))  # Forme pas à connaître mais très utile pour afficher un texte complexe.
print("t2 = {} +/- {}".format(t2_m, t2_u))
print("d1 = {} +/- {}".format(d1_m, d1_u))
print("d2 = {} +/- {}".format(d2_m, d2_u))
print("c = {} +/- {}".format(c_m, c_u))

2.2.3. Rendez-compte de votre mesure#

L’affichage précédent n’est pas acceptable car :

il affiche trop de chiffres
il ne donne pas l’unité.

Un résultat de mesure unique avec incertitude doit s’écrire sous la forme :

\[ G = (G_{mes} \pm u(G)) \rm{Unités} \]

Vous devez respectez les contraintes suivantes :

L’incertitude de mesure doit avoir 2 chiffres significatifs
La valeur mesure doit avoir la même précision que l’incertitude ne mesure.

Rendre-compte de votre résultat de mesure.

\[ c = (Resultat de mesurage \pm Incertitude) (Facultatif: \times Puissance de 10) \rm{Unité} \]

2.3. Données théoriques#

D’après la littérature, la célérité du son dépend de la température et peut être approximée par la fonction :

\[ c_{air} = 331,5 + 0,607 \theta \]

autour de la température ambiante où \(\theta\) est la température en Celsius.

(Robert N. Compton et Michael A. Duncan, Laser Experiments for Chemistry and Physics)

Ecrire une fonction cel_T(T) qui prend comme argument un flottant (température T) et qui renvoie un flottant : la célérité(en m/s). L’utiliser pour estimer la celérité attendue.

Estimer, on moyen d’une simulation Monte-Carlo l’incertitude sur la célérité attendue en supposant que la seule source d’incertitude vient de la mesure de la température.

Calculer l’écart normalisé entre la célérité estimée par votre mesure et celle donnée par la littérature. Conclure quant à la compatibilité entre votre expérience et le modèle proposé.

Pour rappel, l’écart-normalisé est:

\[ EN = \frac{\left\vert c_{exp} - c_{attendue} \right\vert}{\sqrt{u(c_{exp})^2 + u(c_{attendue})^2}} \]

def cel_T(T):
    """Fonction renvoie la célérité pour une température T"""
    return True

"""Estimation de c_attendue"""

"""Estimation de l'incertitude sur c_atttendue"""

"""Calculer l'écart normalisé."""
en = 0

print(en)

Important

Que ce soit ici en codant sous Python ou par écrit en analysant un ensemble de résultats ou une courbe, l’exploitation n’est JAMAIS automatique et demande TOUJOURS de réfléchir en détail à vos résultats.

Méthodes expérimentales - Introduction

(TP) Application à l’étude des ultrasons. (1h)

Contents